
分析 (1)在解答时,应充分考虑自变量的范围不同销售的价格表达形式不同,分情况讨论即可获得日销售金额y关于时间t的函数关系式;
(2)根据分段函数不同段上的表达式,分别求最大值最终取较大者分析即可获得问题解答.
解答 解:(1)由题意可知:y=$\left\{\begin{array}{l}{(t+20)(-t+40),(0<t<25,t∈{N}_{+})}\\{(-t+100)(-t+40),(25≤t≤30,t∈{N}_{+})}\end{array}\right.$.
(2)当0<t<25,t∈N+时,y=(t+20)(-t+40)=-t2+20t+800=-(t-10)2+900.
∴t=10(天)时,ymax=900(元),
当25≤t≤30,t∈N+时,y=(-t+100)(-t+40)=t2-140t+4000=(t-70)2-900,
而y=(t-70)2-900,在t∈[25,30]时,函数递减.
∴t=25(天)时,ymax=1125(元).
∵1125>900,∴ymax=1125(元).
故所求日销售金额的最大值为1125元,且在最近30天中的第25天日销售额最大.
点评 本题考查的是分段函数应用类问题.在解答的过程当中充分体现了分类讨论的思想、二次函数球最值得方法以及问题转化的能力.值得同学们体会反思.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
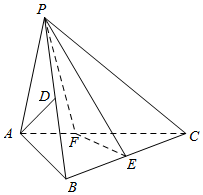 如图,在三棱锥P-ABC中,已知PA=AB,∠ABC为直角,PA⊥BC.点D,E分别为PB,BC的中点.
如图,在三棱锥P-ABC中,已知PA=AB,∠ABC为直角,PA⊥BC.点D,E分别为PB,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数$f(x)=3sin({\frac{x}{2}+\frac{π}{6}})+3$
已知函数$f(x)=3sin({\frac{x}{2}+\frac{π}{6}})+3$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com