
分析 (I)利用数列递推公式可得a1=S1=2k-1,a2=S2-S1=4k-1,可得a2-a1=2k=2,解得k.即可得出.
(II)由题意${b_1}=\frac{8}{3},{b_n}-{b_{n-1}}={2^a}={2^{2n-1}}(n≥2)$,利用累加法与等比数列的求和公式即可得出.
解答 解:(Ⅰ)由题意可得a1=S1=2k-1,a2=S2-S1=4k-1,
∴a2-a1=2k=2,即k=1.
故数列{an}是首项为1,公差为2的等差数列,即an=2n-1.
(Ⅱ)由题意${b_1}=\frac{8}{3},{b_n}-{b_{n-1}}={2^a}={2^{2n-1}}(n≥2)$,
由累加法可得n≥2时,bn=(bn-bn-1)+(bn-1-bn-2)+…+(b2-b1)+b1=${2^2}+{2^5}+…+{2^{2n-1}}+{b_1}=\frac{{{2^3}(1-{4^{n-1}})}}{1-4}+\frac{8}{3}=\frac{{{2^{2n+1}}}}{3}$.
点评 本题考查了数列递推关系、等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:解答题
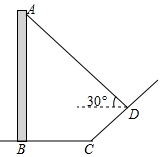 如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC,CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号).
如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC,CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f[${\frac{2}{{2-{a^2}}}}$]<f(${{a^2}-2a+\frac{5}{4}}$) | B. | f[-cos60°]<f(tan30°) | ||
| C. | f[-(cos60°)2]≥f(${{a^2}-2a+\frac{5}{4}}$) | D. | f[-sin45°]>f(-3a+2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{a}$ | B. | $-\sqrt{-a}$ | C. | $\sqrt{-a}$ | D. | $\sqrt{a}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com