
| 1 |
| x |
| 1 |
| x |
| x-1 |
| x2 |
| ax+1 |
| x2 |
| 1 |
| e |
| 1 |
| a |
| 1 |
| a |
| 1 |
| e |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| e |
| 1 |
| e |
|


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
sin3(
| ||||
| sin(3π+α)+cos(4π-α) |
| 5π |
| 2 |
| 3π |
| 2 |
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
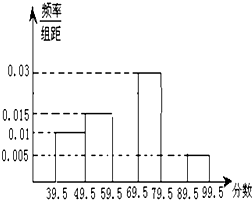 为了解一大片经济林生长情况,随机测量其中的60株的底部周长(单位:cm),规定底部周长60cm及以上优质树木)将周长整理后画出的频率分布表和频率分布直方图如图:观察图形,回答下列问题:
为了解一大片经济林生长情况,随机测量其中的60株的底部周长(单位:cm),规定底部周长60cm及以上优质树木)将周长整理后画出的频率分布表和频率分布直方图如图:观察图形,回答下列问题:| 组距 | 频数 | 频率 |
| [39.5,49.5) | 6 | 0.1 |
| [49.5,59.5) | 0.15 | |
| [59.5,69.5) | 9 | |
| [69.5,79.5) | 18 | |
| [79.5,89.5) | 0.25 | |
| [89.5,99.5) | 3 | 0.05 |
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| sinα+2cosα |
| cosα-sinα |
| 2sin2α+cos2α |
| sinαcosα-cos2α |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com