
分析 (1)根据an+1=Sn+1-Sn化简已知的等式,变形后由等比数列的定义即可证明结论成立;
(2)由(1)和等比数列的通项公式求出an,代入bn=ln$\frac{a_n}{n}$由对数的运算化简后,利用分组求和法和裂项相消法、等差数列的前n项和公式求出Tn.
解答 证明:(1)由${a_{n+1}}=\frac{n+2}{n}{S_n}$及an+1=Sn+1-Sn得,
${S_{n+1}}-{S_n}=\frac{n+2}{n}{S_n}$,整理得nSn+1=2(n+1)Sn,
∴$\frac{{{S_{n+1}}}}{n+1}=2\frac{S_n}{n}$,又$\frac{S_1}{1}=1≠0$,
∴$\left\{{\frac{S_n}{n}}\right\}$是以1为首项,2为公比的等比数列.,…(6分)
(2)由(1)得 $\frac{S_n}{n}={2^{n-1}}$,${S_n}=n•{2^{n-1}}$,
所以${a_{n+1}}=\frac{n+2}{n}{S_n}=\frac{n+2}{n}•n•{2^{n-1}}=(n+2)•{2^{n-1}}$,n∈N*
则 ${a_n}=(n+1)•{2^{n-2}}$,n≥2,
又a1=1也符合上式,所以${a_n}=(n+1)•{2^{n-2}}$,n∈N* …(9分)
∴bn=ln$\frac{a_n}{n}$=ln$\frac{(n+1)•{2}^{n-2}}{n}$=(n-2)ln2+[ln(n+1)-lnn],
∴Tn=ln2(-1+0+1+n-2)+(ln2-ln1)+(ln3-ln2)+…++[ln(n+1)-lnn]
=$\frac{n(-1+n-2)}{2}•ln2+$ln(n+1)
=$\frac{n(n-3)}{2}•ln2+ln(n+1)$ …(12分)
点评 本题考查数列的递推公式的应用,等比数列判断方法:定义法,以及分组求和法和裂项相消法求和方法的应用,属于中档题.


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | [-1,2) | C. | [-1,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
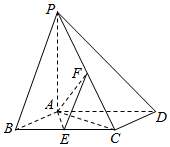 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{16}$-$\frac{y^2}{4}$=1 | B. | $\frac{x^2}{4}$-y2=1 | C. | $\frac{x^2}{9}$-$\frac{y^2}{9}$=1 | D. | $\frac{x^2}{3}$-$\frac{y^2}{3}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com