
| A. | $\frac{x^2}{16}$-$\frac{y^2}{4}$=1 | B. | $\frac{x^2}{4}$-y2=1 | C. | $\frac{x^2}{9}$-$\frac{y^2}{9}$=1 | D. | $\frac{x^2}{3}$-$\frac{y^2}{3}$=1 |
分析 求出抛物线的焦点坐标和准线方程,根据双曲线渐近线的关系建立方程求出a,b的值,即可得到结论.
解答 解:抛物线 y2=2px(p>0)的焦点坐标为($\frac{p}{2}$,0),准线方程为x=-$\frac{p}{2}$,
∵双曲线的一条渐近线与抛物线的准线的交点坐标为(-1,-1),
∴-$\frac{p}{2}$=-1,即p=2,y=$\frac{b}{a}$x过(-1,-1),
即-1=-$\frac{b}{a}$,则$\frac{b}{a}$=1,即b=a,
双曲线的左顶点为(-a,0),抛物线的焦点坐标为(1,0),
∵双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左顶点与抛物线 y2=2px(p>0)的焦点的距离为4,
∴1-(-a)=1+a=4,
则a=3,b=3,
即双曲线的方程为$\frac{x^2}{9}$-$\frac{y^2}{9}$=1,
故选:C.
点评 本题主要考查双曲线方程的求解,根据双曲线和抛物线的方程和性质建立方程关系是解决本题的关键.考查学生的推理能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 10% | B. | 2.5% | C. | 1% | D. | 5% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,已知R(x0,y0)是椭圆$\frac{{y}^{2}}{36}$+$\frac{{x}^{2}}{18}$=1上的一点,从原点O向圆R(x-x0)2+(y-y0)2=12作两条切线,分别交椭圆于P,Q两点.
如图,在平面直角坐标系xOy中,已知R(x0,y0)是椭圆$\frac{{y}^{2}}{36}$+$\frac{{x}^{2}}{18}$=1上的一点,从原点O向圆R(x-x0)2+(y-y0)2=12作两条切线,分别交椭圆于P,Q两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
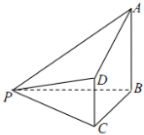 如图,在四棱锥P-ABCD中,AB⊥平面BCP,CD∥平面ABP,AB=BC=CP=BP=2CD=2.
如图,在四棱锥P-ABCD中,AB⊥平面BCP,CD∥平面ABP,AB=BC=CP=BP=2CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{29}{36}$ | B. | $\frac{31}{44}$ | C. | $\frac{36}{55}$ | D. | $\frac{43}{66}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com