
| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
分析 根据向量模长和向量数量积的关系,结合向量数量积的应用进行求解即可.
解答 解:∵$\overrightarrow a$=(1,$\sqrt{3}$),
∴|$\overrightarrow a$|=$\sqrt{1+3}=\sqrt{4}$=2,
∵|${\overrightarrow a$+2$\overrightarrow b}$|=2$\sqrt{3}$,
∴平方得|${\overrightarrow a$|2+4|$\overrightarrow b}$|2+4${\overrightarrow a$•$\overrightarrow b}$=12,
即4+4+4${\overrightarrow a$•$\overrightarrow b}$=12,
则4${\overrightarrow a$•$\overrightarrow b}$=4,${\overrightarrow a$•$\overrightarrow b}$=1,
则cos<${\overrightarrow a$,$\overrightarrow b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{1}{1×2}=\frac{1}{2}$,
则<${\overrightarrow a$,$\overrightarrow b}$>=60°,
故选:B
点评 本题主要考查向量夹角的求解,利用向量数量积的公式和应用是解决本题的关键.


科目:高中数学 来源: 题型:解答题
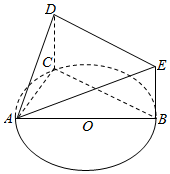 如图,AB是圆O的直径,点C在圆O上,矩形DCBE所在的平面垂直于圆O所在的平面,AB=4,BE=1.
如图,AB是圆O的直径,点C在圆O上,矩形DCBE所在的平面垂直于圆O所在的平面,AB=4,BE=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
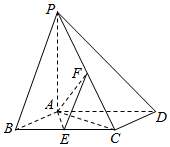 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{16}$-$\frac{y^2}{4}$=1 | B. | $\frac{x^2}{4}$-y2=1 | C. | $\frac{x^2}{9}$-$\frac{y^2}{9}$=1 | D. | $\frac{x^2}{3}$-$\frac{y^2}{3}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com