
分析 (1)直线l的参数方程是$\left\{\begin{array}{l}{x=-1+\frac{3}{5}t}\\{y=-1+\frac{4}{5}t}\end{array}\right.$(t为参数),消去参数t,可得直线l的普通方程.
曲线C的极坐标方程为ρ=$\sqrt{2}$sin(θ+$\frac{π}{4}$),展开可得:ρ2=$\sqrt{2}×\frac{\sqrt{2}}{2}$ρ(sinθ+cosθ),利用互化公式可得曲线C的直角坐标方程.
(2)把直线l的参数方程代入圆的方程可得:5t2-21t+20=0,利用|MN|=|t1-t2|=$\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}$,即可得出.
解答 解:(1)直线l的参数方程是$\left\{\begin{array}{l}{x=-1+\frac{3}{5}t}\\{y=-1+\frac{4}{5}t}\end{array}\right.$(t为参数),消去参数t,可得直线l的普通方程:4x-3y+1=0.
曲线C的极坐标方程为ρ=$\sqrt{2}$sin(θ+$\frac{π}{4}$),展开可得:ρ2=$\sqrt{2}×\frac{\sqrt{2}}{2}$ρ(sinθ+cosθ),可得曲线C的直角坐标方程:
x2+y2=x+y.
(2)把直线l的参数方程代入圆的方程可得:5t2-21t+20=0,
∴t1+t2=$\frac{21}{5}$,t1•t2=4.
∴|MN|=|t1-t2|=$\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}$=$\frac{\sqrt{41}}{5}$.
点评 本题考查了直线参数的应用、极坐标方程化为直角坐标方程、弦长公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{8}$=1 | B. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{8}$=1 | C. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{12}$=1 | D. | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{4}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\sqrt{3}})$ | B. | $({0,1})∪({1,\sqrt{3}})$ | C. | $({1,\sqrt{3}})$ | D. | (0,1)∪(1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
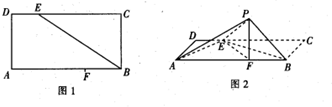 如图1,矩形ABCD中,AB=12,AD=6,E,F分别为CD,AB边上的点,且DE=3,BF=4,将△BCE沿BE折起至△PBE位置(如图2所示),连接AP、EF、PF,其中PF=2$\sqrt{5}$.
如图1,矩形ABCD中,AB=12,AD=6,E,F分别为CD,AB边上的点,且DE=3,BF=4,将△BCE沿BE折起至△PBE位置(如图2所示),连接AP、EF、PF,其中PF=2$\sqrt{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com