
 如图所示,∠BAC=$\frac{2π}{3}$,圆M与AB,AC分别相切于点D,E,AD=1,点P是圆M及其内部任意一点,且$\overrightarrow{AP}$=x$\overrightarrow{AD}$+y$\overrightarrow{AE}$(x,y∈R),则x+y的取值范围是[4-2$\sqrt{3}$,4+2$\sqrt{3}$].
如图所示,∠BAC=$\frac{2π}{3}$,圆M与AB,AC分别相切于点D,E,AD=1,点P是圆M及其内部任意一点,且$\overrightarrow{AP}$=x$\overrightarrow{AD}$+y$\overrightarrow{AE}$(x,y∈R),则x+y的取值范围是[4-2$\sqrt{3}$,4+2$\sqrt{3}$]. 分析 连接MA,MD,求出圆M的半径MD和MA,得出AP的最值,根据等边三角形的性质即可得出x+y的最值.
解答 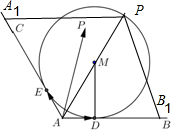 解:连接MA,MD,则∠MAD=$\frac{π}{3}$,MD⊥AD,
解:连接MA,MD,则∠MAD=$\frac{π}{3}$,MD⊥AD,
∵AD=1,∴MD=$\sqrt{3}$,MA=2,
∵点P是圆M及其内部任意一点,
∴2-$\sqrt{3}$≤AP≤2+$\sqrt{3}$,且当A,P,M三点共线时,x+y取得最值,
当AP取得最大值时,以AP为对角线,
以AB,AC为邻边方向作平行四边形AA1PB1,
则△APB1和△APA1是等边三角形,
∴AB1=AA1=AP=2+$\sqrt{3}$,
∴x=y=2+$\sqrt{3}$,
∴x+y的最大值为4+2$\sqrt{3}$,
同理可求出x+y的最小值为4-2$\sqrt{3}$.
故答案为:[4-2$\sqrt{3}$,4+2$\sqrt{3}$].
点评 本题考查了平面向量的几何运算,属于中档题.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{5}{4}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在△ABC中,∠BAC=90°,AB=AC=2,E是边BC的中点,D是边AC上一动点,则$\overrightarrow{AE}$•$\overrightarrow{BD}$的取值范围是( )
如图,在△ABC中,∠BAC=90°,AB=AC=2,E是边BC的中点,D是边AC上一动点,则$\overrightarrow{AE}$•$\overrightarrow{BD}$的取值范围是( )| A. | [0,2] | B. | [-2,0] | C. | [0,2$\sqrt{2}$] | D. | [-2$\sqrt{2}$,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,10) | B. | (4,9) | C. | (5,8) | D. | (6,7) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 2 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 古代的铜钱在铸造时为了方便细加工,常将铜钱穿在一根木棒上,加工时为了较好地固定铜钱,将铜钱当中开成方孔,于是人们也将铜钱称为“孔方兄”.已知图中铜钱是直径为3cm的圆,中间方孔的边长为lcm,若在铜钱所在圆内随机取一点,则此点正好位于方孔中的概率为( )
古代的铜钱在铸造时为了方便细加工,常将铜钱穿在一根木棒上,加工时为了较好地固定铜钱,将铜钱当中开成方孔,于是人们也将铜钱称为“孔方兄”.已知图中铜钱是直径为3cm的圆,中间方孔的边长为lcm,若在铜钱所在圆内随机取一点,则此点正好位于方孔中的概率为( )| A. | $\frac{4}{9π}$ | B. | $\frac{9π}{4}$ | C. | $\frac{4}{3π}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com