
| A. | ($\frac{1}{2}$,1) | B. | (1,2) | C. | ($\frac{3}{2}$,3) | D. | (2,3) |
分析 处理一元三次函数的零点问题可借助其导函数.如本题有两个不同的零点即为其导函数有两个不同的根.
解答 解:∵函数f(x)有且仅有两个不同的零点,
∴f(x)的导函数f′(x)=3x2-6bx,有两个不同的根
由f′(x)=0得x=0或x=2b
∵f(0)=a≠0,
∴f(2b)=0,即$\frac{1}{2}$<b<1
则f(x)有一根是确定的,为2b.
f(x)的另一个根为负的,且f(x)=(x-2b)2(x+b)
∴另一个根为-b.
则|x1-x2|=3b
∴两个根的差的绝对值为($\frac{3}{2}$,3)
故选:C.
点评 本题考查函数求导,及一元二次导函数求根.需要熟练掌握原函数与导函数的关系,由于是选择题,本题属于中档题.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:高中数学 来源: 题型:解答题
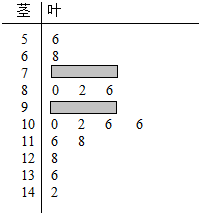 某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:
某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:| 分数段(分) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150) | 总计 |
| 频数 | b | |||||
| 频率 | a | 0.25 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
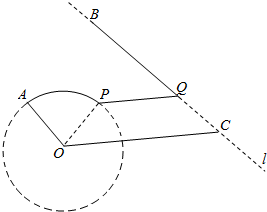 如图,B、C是海岸线l上相距50km的两个海边小城,圆O是半径为10km的某海岛小城的环岛路,A为圆O上的物资中转站,其中∠AOC=$\frac{2}{3}$π,OC=25km,且l∥OA,为使中转站A的物资运往B城,计划从A地沿环岛路至某地P,再沿水路PQ至海岸线l上Q,最后沿海岸线QB至B城修建运输线,其中PQ∥OC,Q在线段BC上.
如图,B、C是海岸线l上相距50km的两个海边小城,圆O是半径为10km的某海岛小城的环岛路,A为圆O上的物资中转站,其中∠AOC=$\frac{2}{3}$π,OC=25km,且l∥OA,为使中转站A的物资运往B城,计划从A地沿环岛路至某地P,再沿水路PQ至海岸线l上Q,最后沿海岸线QB至B城修建运输线,其中PQ∥OC,Q在线段BC上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com