
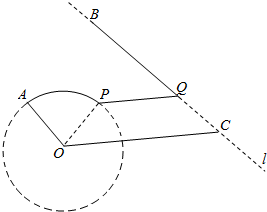
 如图,B、C是海岸线l上相距50km的两个海边小城,圆O是半径为10km的某海岛小城的环岛路,A为圆O上的物资中转站,其中∠AOC=$\frac{2}{3}$π,OC=25km,且l∥OA,为使中转站A的物资运往B城,计划从A地沿环岛路至某地P,再沿水路PQ至海岸线l上Q,最后沿海岸线QB至B城修建运输线,其中PQ∥OC,Q在线段BC上.
如图,B、C是海岸线l上相距50km的两个海边小城,圆O是半径为10km的某海岛小城的环岛路,A为圆O上的物资中转站,其中∠AOC=$\frac{2}{3}$π,OC=25km,且l∥OA,为使中转站A的物资运往B城,计划从A地沿环岛路至某地P,再沿水路PQ至海岸线l上Q,最后沿海岸线QB至B城修建运输线,其中PQ∥OC,Q在线段BC上.分析 (1)设∠POC=θ,求出$\widehat{AP}$=10($\frac{2}{3}$π-θ),PQ=25-10cosθ-$\frac{10\sqrt{3}}{3}$sinθ,CQ=$\frac{20\sqrt{3}}{3}$sinθ,即可求运输线总长度y关于θ的函数;
(2)利用导数求运输线总长度的最小值.
解答 解:(1)由题意,$\widehat{AP}$=10($\frac{2}{3}$π-θ),PQ=25-10cosθ-$\frac{10\sqrt{3}}{3}$sinθ,CQ=$\frac{20\sqrt{3}}{3}$sinθ,
∴y=10($\frac{2}{3}$π-θ)+25-10cosθ-$\frac{10\sqrt{3}}{3}$sinθ+50-$\frac{20\sqrt{3}}{3}$sinθ=$\frac{20π}{3}$+75-10θ-10cosθ-10$\sqrt{3}$sinθ(0<θ<$\frac{2}{3}$π);
(2)y′=-10+10sinθ-10$\sqrt{3}$cosθ=0,
∴20sin(θ-$\frac{π}{3}$)=10,
∴θ=$\frac{π}{2}$,
∴0<θ<$\frac{π}{2}$,函数单调递减,$\frac{π}{2}$<θ<$\frac{2}{3}$π,函数单调递增,
∴θ=$\frac{π}{2}$,运输线总长度y最小,最小值为$\frac{10π}{3}$+75-10$\sqrt{3}$(km).
点评 本题考查利用数学知识解决实际问题,考查导数知识的运用,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,1) | B. | (1,2) | C. | ($\frac{3}{2}$,3) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 钝角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{40}{21}$ | B. | $\frac{20}{21}$ | C. | $\frac{19}{10}$ | D. | $\frac{20}{19}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com