
ЗжЮі ЃЈ1ЃЉЩшЕндіЕШВюЪ§Са{an}ЕФЙЋВюЮЊdЃО0ЃЌЧвa1=1ЃЌЕШБШЪ§Са{bn}ЕФЙЋБШЮЊqЃЌЧвa2=b2ЃЌa5=b3ЃЌa14=b4ЃЎПЩЕУ1+d=b1qЃЌ1+4d=${b}_{1}{q}^{2}$ЃЌ1+13d=${b}_{1}{q}^{3}$ЃЌСЊСЂНтГіМДПЩЕУГіЃЎ
ЃЈ2ЃЉcn=2ЁС3n-1ЃЎПЩЕУan•cn=ЃЈ4n-2ЃЉ•3n-1ЃЎдйРћгУЁАДэЮЛЯрМѕЗЈЁБгыЕШБШЪ§СаЕФЧАnЯюКЭЙЋЪНМДПЩЕУГіЃЎ
НтД№ НтЃКЃЈ1ЃЉЩшЕндіЕШВюЪ§Са{an}ЕФЙЋВюЮЊdЃО0ЃЌЧвa1=1ЃЌЕШБШЪ§Са{bn}ЕФЙЋБШЮЊqЃЌЧвa2=b2ЃЌa5=b3ЃЌa14=b4ЃЎ
Ёр1+d=b1qЃЌ1+4d=${b}_{1}{q}^{2}$ЃЌ1+13d=${b}_{1}{q}^{3}$ЃЌ
СЊСЂНтЕУd=2ЃЌq=3ЃЌb1=1ЃЎ
Ёрan=1+2ЃЈn-1ЃЉ=2n-1ЃЌ
bn=3n-1ЃЎ
ЃЈ2ЃЉЁпan+1=$\frac{{c}_{1}}{{b}_{1}}$+$\frac{{c}_{2}}{{b}_{2}}$+Ё+$\frac{{c}_{n}}{{b}_{n}}$ЃЌ
ЁрЕБn=1ЪБЃЌa2=$\frac{{c}_{1}}{{b}_{1}}$ЃЌНтЕУc1=3ЃЛ
ЕБnЁн2ЪБЃЌan=$\frac{{c}_{1}}{{b}_{1}}$+$\frac{{c}_{2}}{{b}_{2}}$+Ё+$\frac{{c}_{n-1}}{{b}_{n-1}}$ЃЌПЩЕУan+1-an=$\frac{{c}_{n}}{{b}_{n}}$=2ЃЌ
Ёрcn=2ЁС3n-1ЃЎ
Ёрan•cn=ЃЈ4n-2ЃЉ•3n-1ЃЎ
ЁрЪ§Са{an•cn}ЕФЧАnЯюКЭSn=2+6ЁС3+Ё+ЃЈ4n-2ЃЉ•3n-1ЃЎ
3Sn=2ЁС3+6ЁС32+Ё+ЃЈ4n-6ЃЉ•3n-1+ЃЈ4n-2ЃЉ•3nЃЌ
Ёр-2Sn=2+4ЃЈ3+32+Ё+3n-1ЃЉ-ЃЈ4n-2ЃЉ•3n=2+4ЁС$\frac{3ЃЈ{3}^{n-1}-1ЃЉ}{3-1}$-ЃЈ4n-2ЃЉ•3n=ЃЈ4-4nЃЉ•3n-4ЃЌ
НтЕУSn=2+ЃЈ2n-2ЃЉ•3nЃЎ
ЕуЦР БОЬтПМВщСЫЕнЭЦЙиЯЕЕФгІгУЁЂЗжРрЬжТлЫМЯыЗНЗЈЁЂЗжзщЧѓКЭЗНЗЈЁЂЕШБШЪ§СаЕФЭЈЯюЙЋЪНЃЌПМВщСЫЭЦРэФмСІгыМЦЫуФмСІЃЌЪєгкжаЕЕЬтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
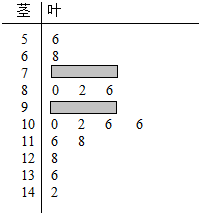 ФГЪ§бЇРЯЪІЖдБОаЃ2013НьИпШ§бЇЩњЕФИпПМЪ§бЇГЩМЈАД1ЃК200НјааЗжВуГщбљГщШЁСЫ20УћбЇЩњЕФГЩМЈЃЌВЂгУОЅвЖЭММЧТМЗжЪ§ШчЭМЫљЪОЃЌЕЋВПЗжЪ§ОнВЛаЁаФЖЊЪЇЃЌЭЌЪБЕУЕНШчЯТЫљЪОЕФЦЕТЪЗжВМБэЃК
ФГЪ§бЇРЯЪІЖдБОаЃ2013НьИпШ§бЇЩњЕФИпПМЪ§бЇГЩМЈАД1ЃК200НјааЗжВуГщбљГщШЁСЫ20УћбЇЩњЕФГЩМЈЃЌВЂгУОЅвЖЭММЧТМЗжЪ§ШчЭМЫљЪОЃЌЕЋВПЗжЪ§ОнВЛаЁаФЖЊЪЇЃЌЭЌЪБЕУЕНШчЯТЫљЪОЕФЦЕТЪЗжВМБэЃК| ЗжЪ§ЖЮЃЈЗжЃЉ | [50ЃЌ70ЃЉ | [70ЃЌ90ЃЉ | [90ЃЌ110ЃЉ | [110ЃЌ130ЃЉ | [130ЃЌ150ЃЉ | змМЦ |
| ЦЕЪ§ | b | |||||
| ЦЕТЪ | a | 0.25 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 2+cosx=4 | BЃЎ | $\sqrt{10}$ЃОІа | CЃЎ | sinx•cosx=sin2x | DЃЎ | sin75ЁуЃОcos14Ёу |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | y2=8x | BЃЎ | x2=4y | CЃЎ | y2=8xЛђx2=-4y | DЃЎ | y2=8xЛђx2=4y |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
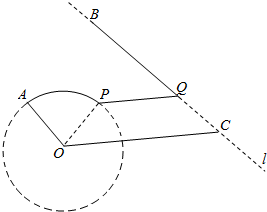 ШчЭМЃЌBЁЂCЪЧКЃАЖЯпlЩЯЯрОр50kmЕФСНИіКЃБпаЁГЧЃЌдВOЪЧАыОЖЮЊ10kmЕФФГКЃЕКаЁГЧЕФЛЗЕКТЗЃЌAЮЊдВOЩЯЕФЮязЪжазЊеОЃЌЦфжаЁЯAOC=$\frac{2}{3}$ІаЃЌOC=25kmЃЌЧвlЁЮOAЃЌЮЊЪЙжазЊеОAЕФЮязЪдЫЭљBГЧЃЌМЦЛЎДгAЕибиЛЗЕКТЗжСФГЕиPЃЌдйбиЫЎТЗPQжСКЃАЖЯпlЩЯQЃЌзюКѓбиКЃАЖЯпQBжСBГЧаоНЈдЫЪфЯпЃЌЦфжаPQЁЮOCЃЌQдкЯпЖЮBCЩЯЃЎ
ШчЭМЃЌBЁЂCЪЧКЃАЖЯпlЩЯЯрОр50kmЕФСНИіКЃБпаЁГЧЃЌдВOЪЧАыОЖЮЊ10kmЕФФГКЃЕКаЁГЧЕФЛЗЕКТЗЃЌAЮЊдВOЩЯЕФЮязЪжазЊеОЃЌЦфжаЁЯAOC=$\frac{2}{3}$ІаЃЌOC=25kmЃЌЧвlЁЮOAЃЌЮЊЪЙжазЊеОAЕФЮязЪдЫЭљBГЧЃЌМЦЛЎДгAЕибиЛЗЕКТЗжСФГЕиPЃЌдйбиЫЎТЗPQжСКЃАЖЯпlЩЯQЃЌзюКѓбиКЃАЖЯпQBжСBГЧаоНЈдЫЪфЯпЃЌЦфжаPQЁЮOCЃЌQдкЯпЖЮBCЩЯЃЎВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com