
分析 (1)利用导数判断目标函数的单调性,从而得到目标函数在相应单调区间上的最大值,进而求解出参数.
(2)考查函数的零点、等差中项等数学概念,需根据题意构造新的函数,并且应用导数得出新构造函数的单调性,从而证明结论.
解答 解:(1)由y=ax+f(x)=ax+lnx,求导,y′=a+$\frac{1}{x}$,x∈(0,e].
当a≥$\frac{1}{e}$时,x∈(0,e],y′>0,则函数y=ax+lnx是单调递增函数,
ymax=a2+lne=ae+1≥0,不符合题意,
若a<-$\frac{1}{e}$,则x∈(0,-$\frac{1}{a}$)时,y′>0,函数y=ax+lnx是单调递增函数,
x∈(-$\frac{1}{a}$,e)时,y′<0,函数y=ax+lnx是单调递减函数,
ymax=-1+ln(-$\frac{1}{a}$)=-4,解得:a=-e3<-$\frac{1}{e}$,
∴a=-e3,
∴实数a的值-e3;
(2)证明:由x1,x2为函数y=ag(2x)+bg(x)-x有两个不同的零点,
不妨设x1<x2,则a${e}^{2{x}_{1}}$+b${e}^{{x}_{1}}$-x1=0,a${e}^{2{x}_{2}}$+b${e}^{{x}_{2}}$-x2=0,
则a(${e}^{2{x}_{1}}$-${e}^{2{x}_{2}}$)+b(${e}^{{x}_{1}}$-${e}^{{x}_{2}}$)-(x2-x1)=0,
即$\frac{a({e}^{2{x}_{1}}-{e}^{2{x}_{2}})}{{e}^{{x}_{2}}-{e}^{{x}_{1}}}$+b-$\frac{{x}_{2}-{x}_{1}}{{e}^{{x}_{2}}-{e}^{{x}_{1}}}$=0,
则a(${e}^{{x}_{2}}$+${e}^{{x}_{1}}$)+b=$\frac{{x}_{2}-{x}_{1}}{{e}^{{x}_{2}}-{e}^{{x}_{1}}}$,
由${e}^{{x}_{2}}$+${e}^{{x}_{1}}$>2$\sqrt{{e}^{{x}_{2}}{e}^{{x}_{1}}}$=2${e}^{\frac{{x}_{1}+{x}_{2}}{2}}$,
则2a${e}^{\frac{{x}_{1}+{x}_{2}}{2}}$+b<$\frac{{x}_{2}-{x}_{1}}{{e}^{{x}_{2}}-{e}^{{x}_{1}}}$,
∴2a${e}^{{x}_{1}+{x}_{2}}$+b${e}^{\frac{{x}_{1}+{x}_{2}}{2}}$<$\frac{{x}_{2}-{x}_{1}}{{e}^{{x}_{2}}-{e}^{{x}_{1}}}$${e}^{\frac{{x}_{1}+{x}_{2}}{2}}$,
令t=x2-x1>0,G(t)=${e}^{\frac{t}{2}}$-${e}^{-\frac{t}{2}}$-t,
G′(t)=$\frac{1}{2}$${e}^{\frac{t}{2}}$+$\frac{1}{2}$${e}^{-\frac{t}{2}}$-1,
故函数G(t)=${e}^{\frac{t}{2}}$-${e}^{-\frac{t}{2}}$-t,在(0,+∞)上单调递增
G(t)>G(0)=0,
∴${e}^{\frac{{x}_{2}-{x}_{1}}{2}}$-${e-}^{\frac{{x}_{2}-{x}_{1}}{2}}$-(x2-x1)>0,即$\frac{{x}_{2}-{x}_{1}}{{e}^{\frac{{x}_{2}-{x}_{1}}{2}-{e}^{-\frac{{x}_{2}-{x}_{1}}{2}}}}$<1,
又$\frac{{x}_{2}-{x}_{1}}{{e}^{{x}_{2}}-{e}^{{x}_{1}}}$•${e}^{\frac{{x}_{1}+{x}_{2}}{2}}$=$\frac{{x}_{2}-{x}_{1}}{{e}^{{x}_{2}-{x}_{1}}-1}$•${e}^{\frac{{x}_{2}-{x}_{1}}{2}}$=$\frac{{x}_{2}-{x}_{1}}{e\frac{{x}_{2}-{x}_{1}}{2}-e-\frac{{x}_{2}-{x}_{1}}{2}}$,
又∵2ag(2x0)+bg(x0)=2a${e}^{{x}_{1}+{x}_{2}}$+b${e}^{\frac{{x}_{1}+{x}_{2}}{2}}$,
则2ag(2x0)+bg(x0)<f(e)成立,
原式得证.
点评 本题考查导数的综合应用,考查利用导数求函数的单调性及最值,等差中项的应用,考查构造法,考查转化思想,属于中档题.


科目:高中数学 来源: 题型:选择题
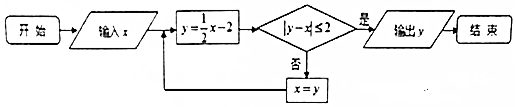
| A. | 2 | B. | -1 | C. | -$\frac{13}{4}$ | D. | -$\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
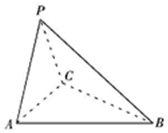 如图,三棱锥P-ABC中,PA=PC,底面ABC为正三角形.
如图,三棱锥P-ABC中,PA=PC,底面ABC为正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
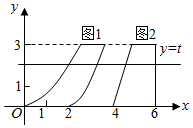 我国南北朝时代的数学家祖暅提出体积的计算原理(祖暅原理):“幂势既同,则积不容 异”.“势’’即是高,“幂”是面积.意思是:如果两等高的几何体在同高处截得两几何体的截面积恒等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个上底为l的梯形,且当实数t取[0,3]上的任意值时,直线y=t被图l和图2所截得的两线段长始终相等,则图l的面积为$\frac{9}{2}$.
我国南北朝时代的数学家祖暅提出体积的计算原理(祖暅原理):“幂势既同,则积不容 异”.“势’’即是高,“幂”是面积.意思是:如果两等高的几何体在同高处截得两几何体的截面积恒等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个上底为l的梯形,且当实数t取[0,3]上的任意值时,直线y=t被图l和图2所截得的两线段长始终相等,则图l的面积为$\frac{9}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 等级 | 1 | 2 | 3 | 4 | 5 |
| 频率 | a | 0.2 | 0.45 | b | c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com