Question

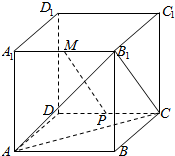
14．如图，在棱长为2 的正方体ABCD-A₁B₁C₁D₁中，M是A₁B₁的中点，点P是侧面CDD₁C₁上的动点，且MP∥截面AB₁C，则线段MP长度的取值范围是（　　）

• A． $[{\sqrt{2}，\sqrt{6}}]$
• B． $[{\sqrt{6}，2\sqrt{2}}]$
• C． $[{\sqrt{6，}2\sqrt{3}}]$
• D． $[{\sqrt{6，}3}]$

Answer 1

分析 取CD的中点N，CC₁的中点R，B₁C₁的中点H，证明平面MNRH∥平面AB₁C，MP?平面MNRH，线段MP扫过的图形是△MNR，通过证明MN²=NR²+MR²，说明∠MRN是直角，可得线段MP长度的取值范围是：（MR，MN），从而得解．

解答 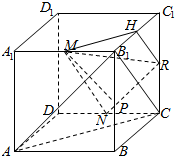解：取CD的中点N，CC₁的中点R，B₁C₁的中点H，
则MN∥B₁C∥HR，MH∥AC，
故平面MNRH∥平面AB₁C，
MP?平面MNRH，线段MP扫过的图形是△MNR，
由AB=2，则MN=2$\sqrt{2}$，NR=$\sqrt{2}$，MR=$\sqrt{6}$，
∴MN²=NR²+MR²，
∴∠MRN是直角，
∴线段MP长度的取值范围是：（MR，MN），即：（$\sqrt{6}$，2$\sqrt{2}$）．
故选：B．

点评 本题考查空间几何体中点的轨迹，直线与平面的位置关系，考查空间想象能力以及计算能力，属于中档题．