
分析 (1)根据直角三角形的性质,求出圆心坐标和半径即可得到结论.
(2)根据直线和圆相切的性质,建立方程关系进行求解即可.
解答 解:(1)∵在直角△ABC中,∠C是直角,顶点A,B的坐标分别为(-4,4),(2,-4),
∴AB是直径,则AB的中点(-1,0),即圆心E(-1,0),
半径R=|BE|=$\sqrt{(-1-2)^{2}+(-4)^{2}}$=$\sqrt{9+16}$=$\sqrt{25}$=5,
则圆E的方程为(x+1)2+y2=25.
(2)∵(4+1)2+102=125>25,
∴点M在圆外,
当切线斜率不存在时,此时切线方程为x=4,到圆心的距离d=4-(-1)=5.此时满足直线和圆相切,
当直线斜率存在时,设为k,则切线方程为y-10=k(x-4),
即kx-y+10-4k=0,
则圆心到直线的距离d=$\frac{|-k+10-4k|}{\sqrt{1+{k}^{2}}}$=$\frac{|10-5k|}{\sqrt{1+{k}^{2}}}$=5,
即|2-k|=$\sqrt{1+{k}^{2}}$,平方得4-4k+k2=1+k2,
即4k=3,
则k=$\frac{3}{4}$,此时切线方程为3x-4y+28=0,
综上求过点M(4,10)且与圆E相切的直线的方程为3x-4y+28=0或x=4.
点评 本题主要考查圆的标准方程以及直线和圆的切线,利用直线和圆的位置关系是解决本题的关键.


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
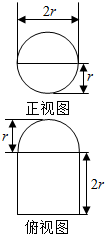 圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示,若该几何体的表面积为4+5π,则半径r=1.
圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示,若该几何体的表面积为4+5π,则半径r=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 动物和植物的机体都是细胞组成的;植物细胞中有细胞核,所以动物细胞中也有细胞核.此推理是归纳推理 | |
| B. | “由圆的性质推出球的有关性质”是类比推理 | |
| C. | 观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…则可得到a10+b10=122 | |
| D. | 函数f(x)是可导函数,已知f′(a)=0则a为f(x)的极值点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
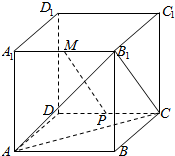 如图,在棱长为2 的正方体ABCD-A1B1C1D1中,M是A1B1的中点,点P是侧面CDD1C1上的动点,且MP∥截面AB1C,则线段MP长度的取值范围是( )
如图,在棱长为2 的正方体ABCD-A1B1C1D1中,M是A1B1的中点,点P是侧面CDD1C1上的动点,且MP∥截面AB1C,则线段MP长度的取值范围是( )| A. | $[{\sqrt{2},\sqrt{6}}]$ | B. | $[{\sqrt{6},2\sqrt{2}}]$ | C. | $[{\sqrt{6,}2\sqrt{3}}]$ | D. | $[{\sqrt{6,}3}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2:1 | B. | 5:2 | C. | 1:4 | D. | 3:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{2}{3},\;\frac{4}{3}}]$ | B. | $[{\frac{2}{3},\;+∞})$ | C. | $[{\frac{4}{3},\;+∞})$ | D. | $[{\frac{4}{3},\;+∞}]∪\left\{{\frac{2}{3}}\right\}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com