
 如图长方体ABCD-A1B1C1D1中,AB=AA1=1,BC=$\sqrt{2}$,M是AD的中点,N是B1C1中点.
如图长方体ABCD-A1B1C1D1中,AB=AA1=1,BC=$\sqrt{2}$,M是AD的中点,N是B1C1中点.分析 (1)以D为原点,建立空间直角坐标系D-xyz,求出$\overrightarrow{N{A}_{1}}$=($\frac{\sqrt{2}}{2}$,-1,0),$\overrightarrow{CM}$=($\frac{\sqrt{2}}{2}$,-1,0),可得$\overrightarrow{N{A}_{1}}$=$\overrightarrow{CM}$,即可证明NA1∥CM;
(2)$\overrightarrow{{D}_{1}B}$•$\overrightarrow{MN}$=0+1-1=0,$\overrightarrow{{D}_{1}B}$•$\overrightarrow{CM}$=0,即可证明D1B⊥平面A1MCN,从而平面A1MCN⊥平面A1BD1.
(3)由(2)得B到平面A1MCN的距离为d=$\frac{B{D}_{1}}{2}$=1,A1B=$\sqrt{2}$,即可求直线A1B和平面A1MCN所成角.
解答 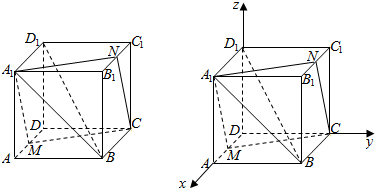 证明:(1)以D为原点,建立空间直角坐标系D-xyz,则B($\sqrt{2}$,1,0),A($\sqrt{2}$,0,1),D1(0,0,1),C(0,1,0),M($\frac{\sqrt{2}}{2}$,0,0),N($\frac{\sqrt{2}}{2}$,1,1),
证明:(1)以D为原点,建立空间直角坐标系D-xyz,则B($\sqrt{2}$,1,0),A($\sqrt{2}$,0,1),D1(0,0,1),C(0,1,0),M($\frac{\sqrt{2}}{2}$,0,0),N($\frac{\sqrt{2}}{2}$,1,1),
∴$\overrightarrow{N{A}_{1}}$=($\frac{\sqrt{2}}{2}$,-1,0),$\overrightarrow{CM}$=($\frac{\sqrt{2}}{2}$,-1,0),
∴$\overrightarrow{N{A}_{1}}$=$\overrightarrow{CM}$,
∴NA1∥CM;
(2)∵$\overrightarrow{{D}_{1}B}$=($\frac{\sqrt{2}}{2}$,1,-1),$\overrightarrow{MN}$=(0,1,1),$\overrightarrow{CM}$=($\frac{\sqrt{2}}{2}$,-1,0),
∴$\overrightarrow{{D}_{1}B}$•$\overrightarrow{MN}$=0+1-1=0,$\overrightarrow{{D}_{1}B}$•$\overrightarrow{CM}$=0,
∴D1B⊥MN,D1B⊥CM,
又MN∩CM=M,
∴D1B⊥平面A1MCN,又D1B?平面A1BD1,
∴平面A1MCN⊥平面A1BD1.
(3)由(2)得B到平面A1MCN的距离为d=$\frac{B{D}_{1}}{2}$=1,A1B=$\sqrt{2}$,
∴直线A1B和平面A1MCN所成角的正弦值为$\frac{d}{{A}_{1}B}$=$\frac{\sqrt{2}}{2}$,
∴直线A1B和平面A1MCN所成角为$\frac{π}{4}$.
点评 本题考查平面与平面垂直的判定,考查空间向量的运用,正确求出向量的坐标是关键.


科目:高中数学 来源: 题型:选择题
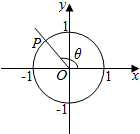
| A. | -$\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | -$\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 上春晚次数x(单位:次) | 1 | 2 | 4 | 6 | 8 |
| 粉丝数量y(单位:万人) | 5 | 10 | 20 | 40 | 80 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
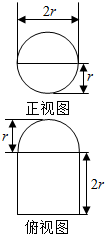 圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示,若该几何体的表面积为4+5π,则半径r=1.
圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示,若该几何体的表面积为4+5π,则半径r=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
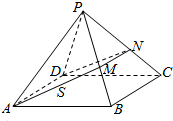 在四棱锥P-ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,底面是正方形(如图),在棱PB,PC上各有一点M、N,且四边形AMND的周长最小,点S从A出发依次沿四边形AM,MN,ND运动至点D,记点S行进的路程为x,棱锥S-ABCD的体积为V(x),则函数V(x)的图象是( )
在四棱锥P-ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,底面是正方形(如图),在棱PB,PC上各有一点M、N,且四边形AMND的周长最小,点S从A出发依次沿四边形AM,MN,ND运动至点D,记点S行进的路程为x,棱锥S-ABCD的体积为V(x),则函数V(x)的图象是( )| A. | 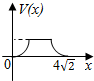 | B. | 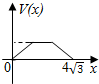 | C. | 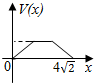 | D. | 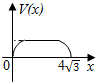 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 动物和植物的机体都是细胞组成的;植物细胞中有细胞核,所以动物细胞中也有细胞核.此推理是归纳推理 | |
| B. | “由圆的性质推出球的有关性质”是类比推理 | |
| C. | 观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…则可得到a10+b10=122 | |
| D. | 函数f(x)是可导函数,已知f′(a)=0则a为f(x)的极值点 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
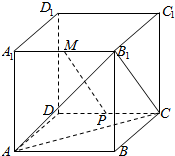 如图,在棱长为2 的正方体ABCD-A1B1C1D1中,M是A1B1的中点,点P是侧面CDD1C1上的动点,且MP∥截面AB1C,则线段MP长度的取值范围是( )
如图,在棱长为2 的正方体ABCD-A1B1C1D1中,M是A1B1的中点,点P是侧面CDD1C1上的动点,且MP∥截面AB1C,则线段MP长度的取值范围是( )| A. | $[{\sqrt{2},\sqrt{6}}]$ | B. | $[{\sqrt{6},2\sqrt{2}}]$ | C. | $[{\sqrt{6,}2\sqrt{3}}]$ | D. | $[{\sqrt{6,}3}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①④ | D. | ③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com