
分析 (1)根据函数奇偶性的定义判断即可;(2)根据函数单调性的定义判断其单调性,从而求出函数的最小值,求出m的范围.
解答 解:(1)在函数f(x)的定义域R上任取一自变量x
因为$f(-x)=\frac{a}{{{a^2}-1}}({a^{-x}}-{a^x})$=-f(x),
所以函数f(x)为奇函数;┅(3分)
(2)当a>1时,在[-1,1]上任取x1,x2,令x1<x2,
$f({x_1})-f({x_2})=\frac{a}{{{a^2}-1}}({{a^{x_1}}-{a^{-{x_1}}}-{a^{x_2}}+{a^{-{x_2}}}})$
=$\frac{a}{{{a^2}-1}}({{a^{x_1}}-{a^{x_2}}})({1+\frac{1}{{{a^{x_1}}{a^{x_2}}}}})$,
∵0≤x1<x2≤1,
∴f(x1)-f(x2)<0
所以函数f(x)在x∈[-1,1]时为增函数,┅(4分)
当0<a<1时,同理可证函数f(x)在x∈[-1,1]时为增函数,
$f{(x)_{min}}=f(-1)=\frac{a}{{{a^2}-1}}({a-{a^{-1}}})=1$,
所以m≤1┅(3分)
点评 本题考查了函数恒成立问题,考查函数的单调性、奇偶性问题,是一道基础题.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:选择题
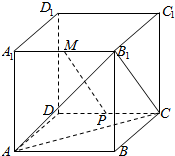 如图,在棱长为2 的正方体ABCD-A1B1C1D1中,M是A1B1的中点,点P是侧面CDD1C1上的动点,且MP∥截面AB1C,则线段MP长度的取值范围是( )
如图,在棱长为2 的正方体ABCD-A1B1C1D1中,M是A1B1的中点,点P是侧面CDD1C1上的动点,且MP∥截面AB1C,则线段MP长度的取值范围是( )| A. | $[{\sqrt{2},\sqrt{6}}]$ | B. | $[{\sqrt{6},2\sqrt{2}}]$ | C. | $[{\sqrt{6,}2\sqrt{3}}]$ | D. | $[{\sqrt{6,}3}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{2}{3},\;\frac{4}{3}}]$ | B. | $[{\frac{2}{3},\;+∞})$ | C. | $[{\frac{4}{3},\;+∞})$ | D. | $[{\frac{4}{3},\;+∞}]∪\left\{{\frac{2}{3}}\right\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 2或4 | D. | 4或8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形或锐角三角形 | D. | 钝角三角形或直角三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com