
分析 (I)由题意分别求得D、F和P点坐标,根据向量加法的坐标表示求得a和b的关系、由椭圆的性质a2=b2+c2及e=$\frac{c}{a}$即可求得e;
(II)由c=3,即可求得椭圆方程,并求得过点A的直线方程,代入椭圆方程,求得关于x的一元二次方程,由△>0求得k的取值范围,利用韦达定理,表示出$\overrightarrow{CM}$•$\overrightarrow{CN}$,令$\overrightarrow{CM}$•$\overrightarrow{CN}$=u,(整理68+4n2-32n-4u)k2+n2-u-12=0,对任意k∈(-$\frac{3}{4}$,$\frac{3}{4}$)都成立,求得关于n和u的二元一次方程组,即可求得n的值,求得C点坐标.
解答 解:(I)由题意可知:A($\frac{{a}^{2}}{c}$,0),B(0,b),
直线AB的方程是:$\frac{cx}{{a}^{2}}+\frac{y}{b}=1$,将x=c代入,得y=$\frac{{b}^{2}}{{a}^{2}}$,
∴D(0,$\frac{{b}^{2}}{{a}^{2}}$),将x=c代入$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,得y=±$\frac{{b}^{2}}{a}$(舍负),
∴P(0,$\frac{{b}^{2}}{{a}^{2}}$),
∵2$\overrightarrow{OD}$=$\overrightarrow{OF}$+$\overrightarrow{OP}$,
∴2(0,$\frac{{b}^{2}}{{a}^{2}}$)=(c,0)+(0,$\frac{{b}^{2}}{{a}^{2}}$),整理得:$\frac{2{b}^{2}}{{a}^{2}}$=$\frac{{b}^{2}}{a}$,即a=2b,
∵a2=b2+c2,
∴e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,
椭圆的离心率$\frac{\sqrt{3}}{2}$;
(II)当c=3时,椭圆的方程为:$\frac{{x}^{2}}{12}+\frac{{y}^{2}}{3}=1$,过A(4,0)的直线方程为y=k(x-4),
将直线方程代入椭圆方程消去y,整理得:(1+4k2)x2-32k2x+64k2-12=0,
∴△=(-32k2)-4(1+4k2)(64k2-12)=-4(16k2-12)>0,
解得:k2<$\frac{3}{4}$,
假设存在点C(n,0),使得$\overrightarrow{CM}$•$\overrightarrow{CN}$为常数,设M(x1,y1),N(x2,y2),
由韦达定理可知:x1+x2=$\frac{32{k}^{2}}{1+4{k}^{2}}$,x1•x2=$\frac{64{k}^{2}-12}{1+4{k}^{2}}$,
$\overrightarrow{CM}$•$\overrightarrow{CN}$=(x1-n,y1)•(x2-n,y2),
=(x1-n)•(x2-n)+y1•y2,
=(x1-n)•(x2-n)+k2(x1-4)(x2-4),
=(1+k2)x1•x2-(n+4k2)(x1+x2)+n2+16k2,
=(1+k2)×$\frac{32{k}^{2}}{1+4{k}^{2}}$-(n+4k2)×$\frac{64{k}^{2}-12}{1+4{k}^{2}}$+n2+16k2=u,
整理得:(68+4n2-32n-4u)k2+n2-u-12=0,对任意k2<$\frac{3}{4}$都成立,
∴$\left\{\begin{array}{l}{68+4{n}^{2}-32n-4u=0}\\{{n}^{2}-u-12=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{n=\frac{29}{8}}\\{u=\frac{73}{64}}\end{array}\right.$,
故在x轴上存在点($\frac{29}{8}$,0)使为常数.
点评 本题考查椭圆的标准方程及简单性质,考查一元二方程根与系数的关系,向量的坐标表示,考查分析问题、解决问题及计算能力,属于难题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
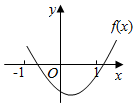 已知函数f(x)=(x-a)(x-b)(其中a>b)的图象如图所示,则函数g(x)=loga(x+b)的大致图象是( )
已知函数f(x)=(x-a)(x-b)(其中a>b)的图象如图所示,则函数g(x)=loga(x+b)的大致图象是( )| A. | 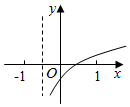 | B. |  | C. | 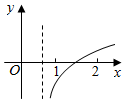 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | B?A | B. | B?A | C. | A?B | D. | A?B |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{15}{4}$ | B. | $\frac{15}{2}$ | C. | -$\frac{15}{4}$ | D. | -$\frac{15}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36种 | B. | 54种 | C. | 72种 | D. | 118种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com