
分析 得到m+(4-m2)i=2cos x+(λ+3sin x)i,由复数相等的条件得$\left\{\begin{array}{l}{m=2cosx}\\{4{-m}^{2}=λ+3sinx}\end{array}\right.$,表示出λ,结合三角函数的性质求出λ的范围即可.
解答 解:若M∩N⊆M,M∩N≠∅,
所以m+(4-m2)i=2cos x+(λ+3sin x)i,
由复数相等的条件得$\left\{\begin{array}{l}{m=2cosx}\\{4{-m}^{2}=λ+3sinx}\end{array}\right.$,
所以λ=4-m2-3sinθ,
=4-4cos2x-3sinx,
=4${(sinx-\frac{3}{8})}^{2}$-$\frac{9}{16}$,
因为-1≤sinθ≤1.
所以当sinx=$\frac{3}{8}$时,λmin=-$\frac{9}{16}$,
当sinθ=-1时,λmax=7,所以-$\frac{9}{16}$≤λ≤7.
点评 如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等,即:如果a,b,c,d∈R,那么a+bi=c+di?a=c,b=d.特殊地,a,b∈R时,a+bi=0?a=0,b=0.复数相等的充要条件,提供了将复数问题化归为实数问题解决的途径.


科目:高中数学 来源: 题型:选择题
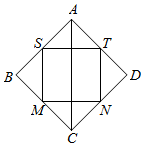 如图,记正方形ABCD四条边的中点为S、M、N、T,连接四个中点得小正方形SMNT.将正方形ABCD、正方形SMNT绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1,V2,则V1:V2=( )
如图,记正方形ABCD四条边的中点为S、M、N、T,连接四个中点得小正方形SMNT.将正方形ABCD、正方形SMNT绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1,V2,则V1:V2=( )| A. | 8:1 | B. | 2:1 | C. | 4:3 | D. | 8:3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
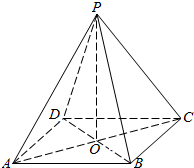 如图,O为正四棱锥P-ABCD的底面中心,该棱锥的侧棱长和底面边长都是2.试求:
如图,O为正四棱锥P-ABCD的底面中心,该棱锥的侧棱长和底面边长都是2.试求:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{6}{5}$ | B. | $\frac{9}{5}$ | C. | $\frac{8}{5}$ | D. | $\frac{7}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com