练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．设{an}是公差为2的等差数列，bn=a${\;}_{{2}^{n}}$，若{bn}为等比数列，则b1+b2+b3+b4+b5=（　　）
    A．142B．124C．128D．144

    分析 由已知得an=a1+（n-1）×2=a1+2n-2，且（a4）2=a2•a8，从而a1=2，${b}_{n}={a}_{{2}^{n}}$=2+2×2n-2=2n+1，由此能求出b1+b2+b3+b4+b5的值．

    解答 解：∵{an}是公差为2的等差数列，bn=a${\;}_{{2}^{n}}$，
    ∴an=a1+（n-1）×2=a1+2n-2，
    ∵{bn}为等比数列，
    ∴${{b}_{2}}^{2}={b}_{1}{b}_{3}$．∴（a4）2=a2•a8，
    ∴$（{a}_{1}+8-2）^{2}$=（a1+4-2）（a1+16-2），
    解得a1=2，
    ∴${b}_{n}={a}_{{2}^{n}}$=2+2×2n-2=2n+1
    b1+b2+b3+b4+b5=22+23+24+25+26=124．
    故选：B．

    点评 本题考查等比数列的前5项和的求法，是基础题，解题时要认真审题，注意等差数列、等比数列的性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    3．在直角坐标系xOy中，椭圆C1：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右焦点分别为F1，F2，且椭圆C1经过点A（1，$\frac{3}{2}$），同时F2也是抛物线C2：y2=4x的焦点．
    （Ⅰ）求椭圆C1的方程；
    （Ⅱ）E，F是椭圆C1上两个动点，如果直线AE与AF的斜率互为相反数，证明直线EF的斜率为定值，并求出这个定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．设△ABC的内角A，B，C分别对应边a，b，c．若c2=（a-b）2+6，${S_{△ABC}}=\frac{3}{2}\sqrt{3}$，则角C=（　　）
    A．$\frac{π}{3}$B．$\frac{π}{6}$C．$\frac{3}{4}π$D．$\frac{2}{3}π$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知函数f（x）是定义在R上的奇函数，其导函数为f′（x），若对任意实数x都有x2f′（x）＞2xf（-x），则不等式x2f（x）＜（3x-1）2f（1-3x）的解集是（　　）
    A．（$\frac{1}{4}$，+∞）B．（0，$\frac{1}{4}$）C．（-∞，$\frac{1}{4}$）D．（-∞，$\frac{1}{4}$）∪（$\frac{1}{4}$，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．在平面直角坐标系xOy中，曲线C1的参数方程为$\left\{\begin{array}{l}{x=1+2cosα}\\{y=\sqrt{3}sinα}\end{array}\right.$（α为参数），将曲线C1上所有点的横坐标缩短为原来的$\frac{1}{2}$，纵坐标缩短为原来的$\frac{\sqrt{3}}{3}$，得到曲线C2，在以坐标原点O为极点，x轴的正半轴为极轴的极坐标系中，直线l的极坐标方程为4ρsin（θ+$\frac{π}{3}$）+$\sqrt{3}$=0．
    （1）求曲线C2的极坐标方程及直线l与曲线C2交点的极坐标；
    （2）设点P为曲线C1上的任意一点，求点P到直线l的距离的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

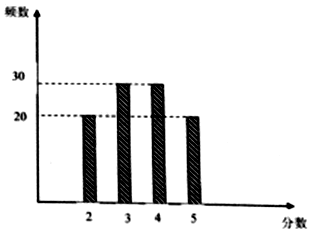    18．某校后勤处为跟踪调查该校餐厅的当月的服务质量，兑现奖惩，从就餐的学生中随机抽出100位学生对餐厅服务质量打分（5分制），得到如图柱状图．
    （Ⅰ）从样本中任意选取2名学生，求恰好有1名学生的打分不低于4分的概率；
    （Ⅱ）若以这100人打分的频率作为概率，在该校随机选取2名学生进行打分（学生打分之间相互独立）记X表示两人打分之和，求X的分布列和E（X）．
    （Ⅲ）根据（Ⅱ）的计算结果，后勤处对餐厅服务质量情况定为三个等级，并制定了对餐厅相应的奖惩方案，如表所示，设当月奖金为Y（单位：元），求E（Y）．
     服务质量评分X X≤5 6≤X≤8 X≥9
     等级 不好 较好 优良
     奖惩标准（元）-1000 2000 3000

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）上一点到两个焦点的距离分别为10和4，且离心率为2，则该双曲线的虚轴长为（　　）
    A．3B．6C．3$\sqrt{3}$D．6$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．△ABC的三个内角A、B、C所对的边分别为a、b、c，已知a≠b，c=$\sqrt{7}$，且bsinB-asinA=$\sqrt{3}$acosA-$\sqrt{3}$bcosB．
    （Ⅰ）求C；
    （Ⅱ）若△ABC的面积为$\frac{3\sqrt{3}}{2}$，求a与b的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知抛物线y2=4x，过焦点F作直线与抛物线交于点A，B，设|AF|=m，|BF|=n，则m+n的最小值为（　　）
    A．2B．3C．$\sqrt{3}$D．4

    查看答案和解析>>

    同步练习册答案