
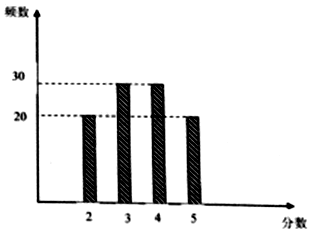
 某校后勤处为跟踪调查该校餐厅的当月的服务质量,兑现奖惩,从就餐的学生中随机抽出100位学生对餐厅服务质量打分(5分制),得到如图柱状图.
某校后勤处为跟踪调查该校餐厅的当月的服务质量,兑现奖惩,从就餐的学生中随机抽出100位学生对餐厅服务质量打分(5分制),得到如图柱状图.| 服务质量评分X | X≤5 | 6≤X≤8 | X≥9 |
| 等级 | 不好 | 较好 | 优良 |
| 奖惩标准(元) | -1000 | 2000 | 3000 |
分析 (Ⅰ)计算“从样本中任意选取2名学生,恰好有一名学生的打分不低于4分”的概率值;
(Ⅱ)由X的可能取值,计算对应的概率值,写出X的分布列,计算数学期望;
(Ⅲ)根据表格写出Y的分布列,计算对应的数学期望值.
解答 解:(Ⅰ)设“从样本中任意选取2名学生,求恰好有一名学生的打分不低于4分”为事件A,
则P(A)=$\frac{{C}_{50}^{1}{•C}_{50}^{1}}{{C}_{100}^{2}}$=$\frac{50}{99}$≈0.51;…(3分)
(Ⅱ)X的可能取值为4,5,6,7,8,9,10;
则P(X=4)=0.2×0.2=0.04,
P(X=5)=2×0.2×0.3=0.12,
P(X=6)=2×0.2×0.3+0.3×0.3=0.21,
P(X=7)=2×0.3×0.3+2×0.2×0.2=0.26,
P(X=8)=2×0.2×0.3+0.3×0.3=0.21,
P(X=9)=2×0.2×0.3=0.12,
P(X=10)=0.2×0.2=0.04;
X的分布列如下:
| X | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| P | 0.04 | 0.12 | 0.21 | 0.26 | 0.21 | 0.12 | 0.04 |
| Y | -1000 | 2000 | 3000 |
| P | 0.16 | 0.68 | 0.16 |
点评 本题考查了频率分布直方图与离散型随机变量的分布列和数学期望的计算问题,是综合性题目.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C;$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>c)的左、右焦点分别为F1(-c,0)、F2(c,0),过原点O的直线(与x轴不重合)与椭圆C相交于D、Q两点,且|DF1|+|QF1|=4,P为椭圆C上的动点,△PF1F2的面积的最大值为$\sqrt{3}$.
已知椭圆C;$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>c)的左、右焦点分别为F1(-c,0)、F2(c,0),过原点O的直线(与x轴不重合)与椭圆C相交于D、Q两点,且|DF1|+|QF1|=4,P为椭圆C上的动点,△PF1F2的面积的最大值为$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 142 | B. | 124 | C. | 128 | D. | 144 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | i | B. | -i | C. | 1+i | D. | 1-i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com