练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．已知x∈R，则“x＞2”是“x2-3x+2＞0”成立的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    分析 根据不等式的关系，结合充分条件和必要条件的定义进行判断即可．

    解答 解：由x2-3x+2＞0得x＞2或x＜-1，
    则“x＞2”是“x2-3x+2＞0”成立的充分不必要条件，
    故选：A

    点评 本题主要考查充分条件和必要条件的判断，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    13．已知（a$\sqrt{x}$+$\frac{\sqrt{3}}{x}$）6（a＞0）展开式中的常数项是5，则a=$\frac{\sqrt{3}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知向量$\overrightarrow{a}$=（1，0），$\overrightarrow{b}$=（0，1），则下列向量中与向量2$\overrightarrow{a}$+$\overrightarrow{b}$垂直的是（　　）
    A．$\overrightarrow{a}$+$\overrightarrow{b}$B．$\overrightarrow{a}$-$\overrightarrow{b}$C．2$\overrightarrow{a}$-$\overrightarrow{b}$D．$\overrightarrow{a}$-2$\overrightarrow{b}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．执行如图所示的程序框图，则输出的结果是（　　）
    A．8B．13C．21D．34

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

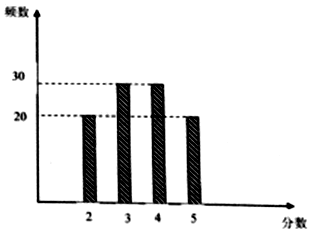    18．某校后勤处为跟踪调查该校餐厅的当月的服务质量，兑现奖惩，从就餐的学生中随机抽出100位学生对餐厅服务质量打分（5分制），得到如图柱状图．
    （Ⅰ）从样本中任意选取2名学生，求恰好有1名学生的打分不低于4分的概率；
    （Ⅱ）若以这100人打分的频率作为概率，在该校随机选取2名学生进行打分（学生打分之间相互独立）记X表示两人打分之和，求X的分布列和E（X）．
    （Ⅲ）根据（Ⅱ）的计算结果，后勤处对餐厅服务质量情况定为三个等级，并制定了对餐厅相应的奖惩方案，如表所示，设当月奖金为Y（单位：元），求E（Y）．
     服务质量评分X X≤5 6≤X≤8 X≥9
     等级 不好 较好 优良
     奖惩标准（元）-1000 2000 3000

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．公元前6世纪，古希腊的毕达哥拉斯学派研究过正五边形和正十边形的作图，发现了黄金分割均为0.618，这一数值也可以表示为m=2sin18°，若m2+n=4，则$\frac{m\sqrt{n}}{2co{s}^{2}27°-1}$=（　　）
    A．8B．4C．2D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知某程序框图如图所示，则执行该程序后输出的结果是（　　）
    A．98B．99C．100D．101

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．已知圆M与y轴相切，圆心在直线y=$\frac{1}{2}$x上，并且在x轴上截得的弦长为2$\sqrt{3}$．则圆M的标准方程为（x-2）2+（y-1）2=4或（x+2）2+（y+1）2=4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知函数$f（x）={（\frac{1}{3}）^x}-{log_2}$x，正实数a，b，c是公差为负数的等差数列，且满足f（a）•f（b）•f（c）＜0，若实数d是方程f（x）=0的一个解，那么下列四个判断：①d＜a；②d＜b；③d＞c；④d＜c中一定成立的个数为（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    同步练习册答案