
分析 (1)求函数的导数根据导数的几何意义先求出a的值,即可求f(x)的单调区间;
(2)利用换元法,利用构造函数即可证明不等式.
解答 解:(1)f′(x)=aln(x+1)+a(x+1)$\frac{1}{x+1}$=a[1+ln(x+1)],-----(2分)
由于f(x)在点(e2-1,f(e2-1))处的切线与直线x+3y+1=0垂直,
所以f′(e2-1)=a(lne2+1)=3,
解得a=1,
∴f(x)=(x+1)ln(x+1),f′(x)=ln(x+1)+1.…(6分)
令f′(x)=0,解得x=$\frac{1}{e}$-1,
由f′(x)>0得x>$\frac{1}{e}$-1,
由f′(x)<0得x<$\frac{1}{e}$-1,
故f(x)的单调递减区间为[-1,$\frac{1}{e}$-1],单调递增区间为($\frac{1}{e}$-1,+∞)…(8分)
证明:(2)令u=em,v=en,
∵m>n>0,∴u>v>0,
要证(1+em)en<(1+en)em.,只需证vln(1+u)<uln(1+v),
这等价于$\frac{ln(1+u)}{u}<\frac{ln(1+v)}{v}$,
令h(x)=$\frac{ln(1+x)}{x}$,x>0,
h′(x)=$\frac{x-(x+1)ln(x+1)}{{x}^{2}(x+1)}$,
令k(x)=x-(1+x)ln(1+x),(x>0),
∵x>0,x+1>1,
∴k′(x)=1-ln(x+1)-1=-ln(x+1)<0,
故k(x)在(0,+∞)单调递减,
∴k(x)<k(0)=0,
故h′(x)<0,故h(x)=$\frac{ln(1+x)}{x}$,x>0,是减函数,
∵u>v>0,
∴h(u)<h(v),
即 $\frac{ln(1+u)}{u}<\frac{ln(1+v)}{v}$,
就是(1+em)${\;}^{{e}^{n}}$<(1+en)${\;}^{{e}^{m}}$.…(14分)
点评 本题主要考查导数的综合应用,利用导数的几何意义求出a的值是解决本题的关键.综合考查导数的应用,综合性较强,运算量较大.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
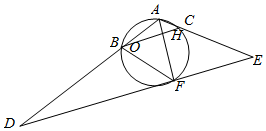 如图,在△ABC中,AH平分∠BAC,交△ABC的外接圆O于点F,过点F作DE∥BC.分别交AB,AC的延长线于D,E两点.
如图,在△ABC中,AH平分∠BAC,交△ABC的外接圆O于点F,过点F作DE∥BC.分别交AB,AC的延长线于D,E两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-π,-$\frac{5π}{6}$] | B. | [-$\frac{5π}{6}$,-$\frac{π}{6}$] | C. | [-$\frac{π}{3}$,0] | D. | [-$\frac{π}{6}$,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com