
���� ֱ��l�IJ���������$\left\{\begin{array}{l}{x=1-\frac{\sqrt{2}}{2}t}\\{y=-4+\frac{\sqrt{2}}{2}t}\end{array}\right.$��tΪ����������ȥ����t���ɻ�Ϊֱ�����귽�̣�����$\left\{\begin{array}{l}{{��}^{2}={x}^{2}+{y}^{2}}\\{x=��cos��}\end{array}\right.$���ɰ�����C�ļ����귽�̦�2-10��cos��+9=0����Ϊֱ�����귽�̣�
��PC��lʱ��|PM|ȡ����Сֵ=$\sqrt{|PC{|}^{2}-{r}^{2}}$��
��� �⣺ֱ��l�IJ���������$\left\{\begin{array}{l}{x=1-\frac{\sqrt{2}}{2}t}\\{y=-4+\frac{\sqrt{2}}{2}t}\end{array}\right.$��tΪ����������Ϊx+y+3=0��
����C�ļ����귽��Ϊ��2-10��cos��+9=0����Ϊx2+y2-10x+9=0���䷽Ϊ��x-5��2+y2=16��
��PC��lʱ��|PM|ȡ����Сֵ=$\sqrt{|PC{|}^{2}-{r}^{2}}$=$\sqrt{��\frac{5+0+3}{\sqrt{2}}��^{2}-16}$=4��
�ʴ�Ϊ��4��
���� ���⿼���˰Ѳ������̻�Ϊ��ͨ���̡������귽�̻�Ϊֱ�����귽�̡��㵽ֱ�ߵľ��빫ʽ��Բ�����ߵ����ʡ����ɶ�����������������������������������е��⣮


 ��ְٷְټ���ϵ�д�
��ְٷְټ���ϵ�д� �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-8��8�� | B�� | ��8��8�� | C�� | ��-8��-8����8��-8�� | D�� | ��-8��8����8��8�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 5 | C�� | 6 | D�� | 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | cosA=cosB | B�� | sinA=sinB | C�� | bcosA=acosB | D�� | acosA=bcosB |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
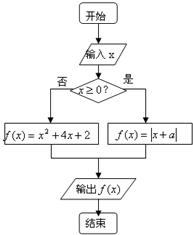
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �٢� | C�� | �ۢ� | D�� | �ڢ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com