

| A. |  | B. |  | C. |  | D. |  |
分析 观察函数y=f(x)的图象得出函数在x=0无意义,故函数y=f(x)•g(x)在x=0无意义,可排除C、D;令x再取很小的正数,从图象可得f(x)的值趋于1,g(x)的值趋于负的无穷大,可得A适合而B不适合,可得答案.
解答 解:根据f(x)和g(x)的图象,可得函数y=g(x)在x=0无意义,∴函数y=f(x)•g(x)在x=0无意义,故排除C、D;
当x是很小的正数时,从图象可得f(x)的值趋于1,g(x)的值趋于负的无穷大,∴f(x)•g(x)趋于负的无穷大,
故A适合而B不适合,
故选:A.
点评 本题主要考查函数的图象的应用,解题的关键是:要从所给的函数图象得出函数成立的信息,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 30种 | B. | 36种 | C. | 42种 | D. | 48种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 合格 | 合计 | |
| 高中组 | 45 | 55 | |
| 初中组 | 15 | ||
| 合计 |
| P(K2>K0) | 0.10 | 0.05 | 0.005 |
| K0 | 2.706 | 3.841 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
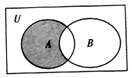 若全集U、集合A、集合B及其关系用韦恩图表示如图所示,则图中阴影表示的集合为( )
若全集U、集合A、集合B及其关系用韦恩图表示如图所示,则图中阴影表示的集合为( )| A. | ∁U(A∩B) | B. | ∁U(A∪B) | C. | A∩(∁UB) | D. | (∁UA)∩B |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com