
| A. | x=$\frac{π}{3}$ | B. | x=$\frac{π}{4}$ | C. | x=$\frac{2π}{3}$ | D. | x=$\frac{π}{6}$ |
分析 利用三角恒等变换化简f(x)的解析式,利用函数y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式,再根据正弦函数的图象的对称性,求得g(x)的一条对称轴.
解答 解:∵$f(x)=cos(x+\frac{2π}{7})+2sin\frac{π}{7}sin(x+\frac{π}{7})=cos[(x+\frac{π}{7})+\frac{π}{7}]+2sin\frac{π}{7}sin(x+\frac{π}{7})$=cos(x+$\frac{π}{7}$)cos$\frac{π}{7}$+sin$\frac{π}{7}$sin(x+$\frac{π}{7}$)=cosx,
把函数f(x)的图象向右平移$\frac{π}{3}$,再把图象上所有点的横坐标扩大到原来的2倍,得到函数g(x)=cos($\frac{1}{2}$x-$\frac{π}{3}$)的图象,
令$\frac{1}{2}$x-$\frac{π}{3}$=kπ,k∈Z,求得x=2kπ+$\frac{2π}{3}$,即对称轴的方程为x=2kπ+$\frac{2π}{3}$,
当k=0时,对称轴的方程为x=2kπ+$\frac{2π}{3}$,k∈Z,
当k=0时,可得g(x)的一条对称轴为 $x=\frac{2π}{3}$,
故选:C.
点评 本题主要考查三角恒等变换,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于中档题.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{2}$ | B. | 4 | C. | 3 | D. | $\frac{12}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1]∪[3,+∞) | B. | [1,3] | C. | (3,+∞) | D. | (-∞,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-cos4x | B. | y=-cosx | C. | y=sin(x+$\frac{π}{4}$) | D. | y=-sinx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
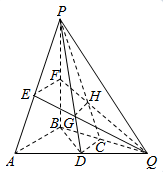 如图所示,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH.
如图所示,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com