
| A. | a=-3,b=~3 | B. | a=0,b=2 | C. | a=-3,b=2 | D. | a=1 b=2 |
分析 将选项依次代入,从而化简求导以确定函数的单调性及极值,从而解得.
解答 解:对于A,当a=-3,b=-3时,
令f(x)=x3-3x-3,
则f′(x)=3x2-3=3(x+1)(x-1),
故f(x)在(-∞,-1)上是增函数,在(-1,1)上是减函数,在(1,+∞)上是增函数;
而f(-1)=-1,f(1)=-5,
故x3+ax+b=0有且仅有一个根;
对于B,当a=0,b=2时,
令f(x)=x3+2,
则f′(x)=3x2≥0,
故f(x)在(-∞,+∞)上是增函数;
故x3+ax+b=0有且仅有一个根;
对于C,当a=-3,b=2时,
令f(x)=x3-3x+2,
则f′(x)=3x2-3=3(x+1)(x-1),
故f(x)在(-∞,-1)上是增函数,在(-1,1)上是减函数,在(1,+∞)上是增函数;
而f(-1)=6,f(1)=0,
故x3+ax+b=0有且仅有两个根;
对于D,当a=1,b=2时,
令f(x)=x3+x+2,
则f′(x)=3x2+1≥1,
故f(x)在(-∞,+∞)上是增函数;
故x3+ax+b=0有且仅有一个根;
故选:C.
点评 本题考查了分类讨论的思想应用及导数的综合应用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
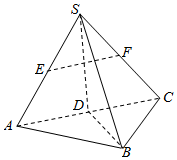 如图,在三棱锥S-ABC中,已知点D、E、F分别为棱AC、SA、SC的中点.
如图,在三棱锥S-ABC中,已知点D、E、F分别为棱AC、SA、SC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{3}{5}i$ | C. | -$\frac{3}{5}$ | D. | $-\frac{3}{5}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③④ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com