
分析 本题考查了直线和圆的有关问题,结合对称性,可以判断出MP和直线y=2x对称,利用切线长相等,可以求出两个全等的三角形的面积.
解答 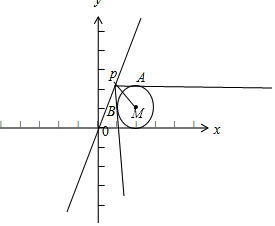 解:直线l1,l2关于直线y=2x对称,
解:直线l1,l2关于直线y=2x对称,
所以PM与直线y=2x垂直,
由点到直线的距离公式可得PM=$\frac{2×2-1}{\sqrt{1+{2}^{2}}}$=$\frac{3}{\sqrt{5}}$,
因为切线长相等,△PAM≌△PBM,
所以四边形的面积为:
2×$\frac{1}{2}×1×\sqrt{(\frac{3}{\sqrt{5}})^{2}-1}=\frac{2\sqrt{5}}{5}$.
故答案为:$\frac{2\sqrt{5}}{5}$.
点评 圆和直线的位置关系是考查的重点和难点,抓住切线长相等和对称性是解题的关键.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-\frac{1}{2},-2})$ | B. | (-1,-2) | C. | $({2,\frac{1}{4}})$ | D. | $({-\frac{1}{2},-4})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
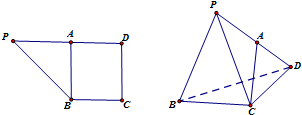 如图,矩形ABCD和直角三角形ABP有共同的边AB,且PA=AD=3,DC=4,沿BD把平面DBP折起,使AC=$\sqrt{7}$.
如图,矩形ABCD和直角三角形ABP有共同的边AB,且PA=AD=3,DC=4,沿BD把平面DBP折起,使AC=$\sqrt{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
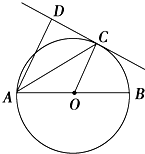 如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.
如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com