
分析 设直线PM,PN的方程,代入椭圆方程即可求得M和N点坐标,即可求得根据直线的斜率公式,化简即可求得$\frac{1}{{k}_{1}}+\frac{1}{{k}_{2}}-\frac{1}{{k}_{3}}$=1.
解答 解:设M(x1,y1),N(x2,y2),直线PM的方程为:y-2=k1(x-1),
联立$\left\{\begin{array}{l}{y={k}_{1}(x-1)+2}\\{{y}^{2}=4x}\end{array}\right.$,化为:y2-$\frac{4}{{k}_{1}}$y+$\frac{8}{{k}_{1}}$-4=0,
解得y=2或y=$\frac{4}{{k}_{1}}$-2.
x1=$\frac{{y}_{1}^{2}}{4}$=$\frac{(2-{k}_{1})^{2}}{{k}_{1}^{2}}$,∴M($\frac{(2-{k}_{1})^{2}}{{k}_{1}^{2}}$,$\frac{4}{{k}_{1}}$-2)
同理可得:N($\frac{(2-{k}_{2})^{2}}{{k}_{1}^{2}}$,$\frac{4}{{k}_{2}}$-2).
∴k3=$\frac{\frac{4}{{k}_{2}}-2-(\frac{4}{{k}_{1}}-2)}{\frac{(2-{k}_{2})^{2}}{{k}_{2}^{2}}-\frac{(2-{k}_{1})^{2}}{{k}_{1}^{2}}}$=$\frac{{k}_{1}{k}_{2}}{({k}_{1}+{k}_{2})-{k}_{1}{k}_{2}}$,
$\frac{1}{{k}_{3}}$=$\frac{{k}_{1}+{k}_{2}}{{k}_{1}{k}_{2}}$-1=$\frac{1}{{k}_{1}}$+$\frac{1}{{k}_{2}}$-1,
∴$\frac{1}{{k}_{1}}+\frac{1}{{k}_{2}}-\frac{1}{{k}_{3}}$=1.
故答案为:1.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查直线的斜率公式,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 28 | B. | 26 | C. | 24 | D. | 22 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
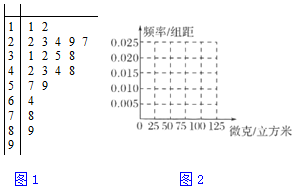
| 组别 | PM2.5浓度(微粒、立方米) | 频数(天) | 频率 |
| 第一组 | (0,25] | 5 | 0.25 |
| 第二组 | (25,50] | 10 | 0.5 |
| 第三组 | (50,75] | 3 | 0.15 |
| 第四组 | (75,100] | 2 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{3}$ | B. | 2 | C. | 1 | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com