
【题目】已知函数![]() ,a∈R.
,a∈R.
(Ⅰ)当a=1时,求曲线y=f(x)在点(0,f(0))处的切线方程;
(Ⅱ)求f(x)的单调区间.
【答案】(Ⅰ)y=0(Ⅱ)单调递减区间为(-1,-![]() ),单调递增区间为(-∞,-1),(-
),单调递增区间为(-∞,-1),(-![]() ,+∞)
,+∞)
【解析】
(Ⅰ)当![]() 时,求出函数
时,求出函数![]() ,利用导数的几何意义求出
,利用导数的几何意义求出![]() 处的切线的斜率,利用点斜式求出切线方程;(II)当
处的切线的斜率,利用点斜式求出切线方程;(II)当![]() 时,令
时,令![]() ,得
,得![]() ,
,![]() ,分三种情况①
,分三种情况①![]() ,②当
,②当![]() ,③当
,③当![]() ,讨论
,讨论![]() 的单调区间.
的单调区间.
(Ⅰ)f(x)的定义域为R,![]() .
.
当a=1时,f′(0)=0,f(0)=0,
所以曲线y=f(x)在点(0,f(0))处的切线方程为y=0.
(Ⅱ)f′(x)=aex(x+1)-x-1=(x+1)(aex-1).
(1)当a≤0时,aex-1<0,
所以当x>-1时,f′(x)<0;当x<-1时,f′(x)>0.
所以f(x)的单调递增区间为(-∞,-1),单调递减区间为(-1,+∞).
(2)当a>0时,令f′(x)=0,得x1=-1,x2=-lna.
①当-lna=-1,即a=e时,f′(x)≥0,
所以f(x)的单调递增区间为(-∞,+∞),无单调递减区间;
②当-lna<-1,即a>e时,
当-lna<x<-1时,f′(x)<0;当x<-lna或x>-1时,f′(x)>0.
所以f(x)的单调递减区间为(-lna,-1),单调递增区间为(-∞,-lna),(-1,+∞);
③当-lna>-1,即0<a<e时,
当-1<x<-lna时,f′(x)<0;当x<-1或x>-lna时,f′(x)>0.
所以f(x)的单调递减区间为(-1,-lna),单调递增区间为(-∞,-1),(-lna,∞).


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:
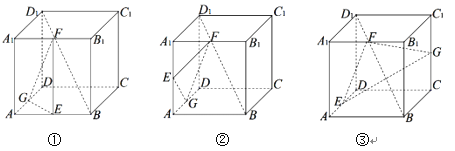
【题目】如图,在下列三个正方体![]() 中,
中,![]() 均为所在棱的中点,过
均为所在棱的中点,过![]() 作正方体的截面.在各正方体中,直线
作正方体的截面.在各正方体中,直线![]() 与平面
与平面![]() 的位置关系描述正确的是
的位置关系描述正确的是
A. ![]() 平面
平面![]() 的有且只有①;
的有且只有①;![]() 平面
平面![]() 的有且只有②③
的有且只有②③
B. ![]() 平面
平面![]() 的有且只有②;
的有且只有②;![]() 平面
平面![]() 的有且只有①
的有且只有①
C. .![]() 平面
平面![]() 的有且只有①;
的有且只有①;![]() 平面
平面![]() 的有且只有②
的有且只有②
D. ![]() 平面
平面![]() 的有且只有②;
的有且只有②;![]() 平面
平面![]() 的有且只有③
的有且只有③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以坐标原点为极点,
),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)若![]() 与
与![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|ax-2|,不等式f(x)≤4的解集为{x|-2≤x≤6}.
(1)求实数a的值;
(2)设g(x)=f(x)+f(x+3),若存在x∈R,使g(x)-tx≤2成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科研人员在对人体脂肪含量和年龄之间关系的研究中,获得了一些年龄和脂肪含量的简单随机样本数据,如下表:
| 26 | 27 | 39 | 41 | 49 | 53 | 56 | 58 | 60 | 61 |
| 14.5 | 17.8 | 21.2 | 25.9 | 26.3 | 29.6 | 31.4 | 33.5 | 35.2 | 34.6 |
根据上表的数据得到如下的散点图.
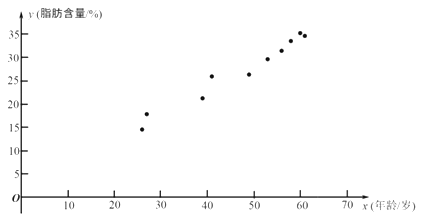
(1)根据上表中的样本数据及其散点图:
(i)求![]() ;
;
(i)计算样本相关系数(精确到0.01),并刻画它们的相关程度.
(2)若![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,求
,求![]() 的值(精确到0.01),并根据回归方程估计年龄为50岁时人体的脂肪含量.
的值(精确到0.01),并根据回归方程估计年龄为50岁时人体的脂肪含量.
附:参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
参考公式:相关系数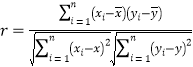
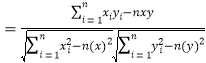
回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为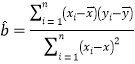 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com