
| A. | 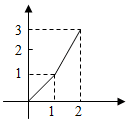 | B. | 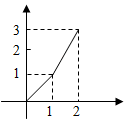 | C. | 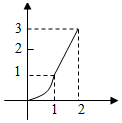 | D. |  |
分析 根据条件先求出OA,AB的表达式,结合直线l的运动位置分析面积的表达形式,进而得到分段函数:$f(t)=\left\{\begin{array}{l}{{t}^{2},0<t≤1}\\{2t-1,1<t≤2}\end{array}\right.$然后分情况即可获得问题的解答.
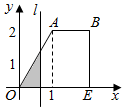
解答 解:当0≤x≤1时,OA:y=2x,
当1≤x≤2时,AB:y=2,
则当0<t≤1时,$f(t)=\frac{1}{2}•t•2t={t}^{2}$,
当1<t≤2 时,$f(t)=1×2×\frac{1}{2}+(t-1)•2=2t-1$;
所以$f(t)=\left\{\begin{array}{l}{{t}^{2},0<t≤1}\\{2t-1,1<t≤2}\end{array}\right.$.
当0<t≤1时,函数的图象是一段抛物线段;
当1<t≤2时,函数的图象是一条线段.
结合不同段上函数的性质,可知选项C符合.
故选:C.
点评 本题考查的是函数的图象和分段函数的综合类问题.在解答的过程当中充分体现了分段函数的知识、分类讨论的思想以及函数图象的知识.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{15}}{3}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$或$\sqrt{2}$ | D. | 3-$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com