
| A. | 10 | B. | 20 | C. | 100 | D. | 120 |
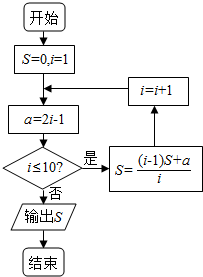
分析 由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量S的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.
解答 解:第一次执行循环体后,a=1,满足继续循环的条件,故S=1,i=2;
第二次执行循环体后,a=3,满足继续循环的条件,故S=2,i=3;
第三次执行循环体后,a=5,满足继续循环的条件,故S=3,i=4;
第四次执行循环体后,a=7,满足继续循环的条件,故S=4,i=5;
第五次执行循环体后,a=9,满足继续循环的条件,故S=5,i=6;
第六次执行循环体后,a=11,满足继续循环的条件,故S=6,i=7;
第七次执行循环体后,a=13,满足继续循环的条件,故S=7,i=8;
第八次执行循环体后,a=15,满足继续循环的条件,故S=8,i=9;
第九次执行循环体后,a=17,满足继续循环的条件,故S=9,i=10;
第十次执行循环体后,a=19,满足继续循环的条件,故S=10,i=11;
第十一次执行循环体后,a=21,不满足继续循环的条件,
故输出的S值为10,
故选:A
点评 本题考查的知识点是程序框图,当循环的次数不多,或有规律时,常采用模拟循环的方法解答.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{6}}}{4}$ | B. | $-\frac{{\sqrt{2}}}{4}$ | C. | $\frac{{\sqrt{6}}}{4}$ | D. | $\frac{{\sqrt{2}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2$\sqrt{3}$ | B. | -$\frac{2\sqrt{3}}{3}$ | C. | 0 | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=lnx2,g(x)=2lnx | B. | f(x)=x,g(x)=($\sqrt{x}$)2 | ||
| C. | f(x)=cosx•tanx,g(x)=sinx | D. | f(x)=x2,g(x)=$\sqrt{{x}^{4}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
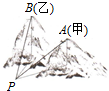 如图,某人在山脚P处测得甲山山顶A的仰角为30°,乙山山顶B的仰角为45°,∠APB的大小为45°,山脚P到山顶A的直线距离为2km,在A处测得山顶B的仰角为30°,则乙山的高度为2km.
如图,某人在山脚P处测得甲山山顶A的仰角为30°,乙山山顶B的仰角为45°,∠APB的大小为45°,山脚P到山顶A的直线距离为2km,在A处测得山顶B的仰角为30°,则乙山的高度为2km.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com