
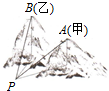
 如图,某人在山脚P处测得甲山山顶A的仰角为30°,乙山山顶B的仰角为45°,∠APB的大小为45°,山脚P到山顶A的直线距离为2km,在A处测得山顶B的仰角为30°,则乙山的高度为2km.
如图,某人在山脚P处测得甲山山顶A的仰角为30°,乙山山顶B的仰角为45°,∠APB的大小为45°,山脚P到山顶A的直线距离为2km,在A处测得山顶B的仰角为30°,则乙山的高度为2km. 分析 根据山顶的仰角可得AC=1,BP=$\sqrt{2}$BD,过A向乙山作垂线,则AB=2(BD-1),在△ABP中使用余弦定理列方程解出BD.
解答 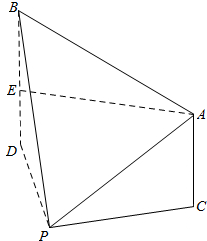 解:假设甲山底部为C,乙山底部为D,过A作AE⊥BD于E.
解:假设甲山底部为C,乙山底部为D,过A作AE⊥BD于E.
由题意可知∠APC=30°,∠BPD=45°,AP=2,
∴AC=AP•sin30°=1,DE=AC=1,设BD=h,则DP=BD=h,BE=h-1,∴BP=$\sqrt{2}$h.
∵∠BAE=30°,∴AB=2BE=2h-2.
在△ABP中,由余弦定理得:cos45°=$\frac{A{P}^{2}+B{P}^{2}-A{B}^{2}}{2AP•BP}$=$\frac{4+2{h}^{2}-({2h-2)}^{2}}{4\sqrt{2}h}$=$\frac{\sqrt{2}}{2}$.
解得h=2.
∴乙山的高度为2km.
故答案为:2.
点评 本题考查了余弦定理在解三角形中的应用,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c,d | B. | d,e | C. | b,e | D. | c,e |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | lg$\frac{2}{5}$ | B. | 1 | C. | -1 | D. | lg$\frac{5}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com