
如图,四棱锥 中,
中, ∥
∥ ,
,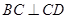 ,侧面
,侧面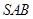 为等边三角形
为等边三角形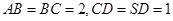
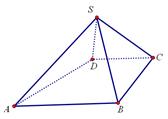
(1)证明:
(2)求AB与平面SBC所成角的正弦值
(1)参考解析;(2)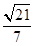
解析试题分析:(1)要证 ,从原图中较难找出线与线的垂直,通过取线段AB的中点E,并连接DE,可求出SE,DE的长结合已知SD的长,可得
,从原图中较难找出线与线的垂直,通过取线段AB的中点E,并连接DE,可求出SE,DE的长结合已知SD的长,可得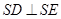 再通过证明
再通过证明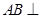 平面
平面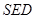 可得
可得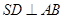 从而可得
从而可得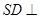 平面
平面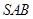
(2)求AB与平面SBC所成角的正弦值,因为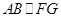 ,所以所求的问题等价于
,所以所求的问题等价于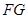 与平面SBC所成角的正弦值 只需要证明平面
与平面SBC所成角的正弦值 只需要证明平面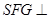 平面,从而作出
平面,从而作出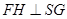 即可得
即可得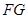 与平面SBC所成角为
与平面SBC所成角为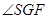 通过解三角形即可得结论
通过解三角形即可得结论 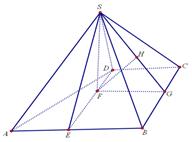
试题解析:(1)证明:取AB中点E,连结DE,则四边形BCDE为矩形,DE=CB=2。
连结SE,则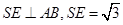
又SD=1,故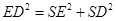
所以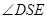 为直角。
为直角。
由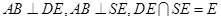 ,得
,得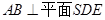 ,所以
,所以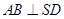
SD与两条相交直线AB、SE都垂直。
所以 6分
6分
(II)由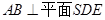 知,
知,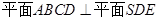
作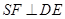 ,垂足为F,
,垂足为F,
则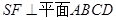 ,
,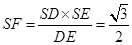
作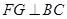 ,垂足为G,则FG=DC=1。
,垂足为G,则FG=DC=1。
连结SG,则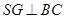
又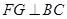 ,
,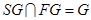 ,
,
故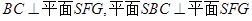 ,
,
作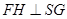 ,H为垂足,则
,H为垂足,则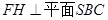
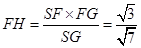
即F到平面SBC的距离为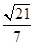
由于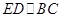 ,所以
,所以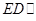 平面
平面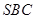 ,E到平面
,E到平面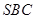 的距离d也为
的距离d也为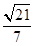 设AB与平面
设AB与平面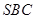 所成的角为
所成的角为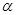 ,则
,则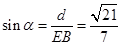
考点:1 线面垂直的知识 2 面面垂直的知识 3 直线与平面所成角的概念 4 线面转化的思想 5 提升探索,分类的能力


科目:高中数学 来源: 题型:解答题
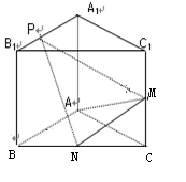
如图,已知三棱锥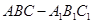 的侧棱与底面垂直,
的侧棱与底面垂直,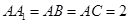 ,
,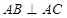 , M、N分别是
, M、N分别是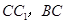 的中点,点P在线段
的中点,点P在线段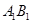 上,且
上,且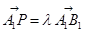 ,
,
(1)证明:无论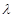 取何值,总有
取何值,总有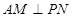 .
.
(2)当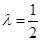 时,求平面
时,求平面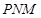 与平面
与平面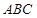 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
(1)求证:PC⊥BC
(2)求点A到平面PBC的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com