
| A�� | �� | B�� | �٢� | C�� | �ڢ� | D�� | �٢ڢ� |
���� ����ֱ�ߵ�б�ʺ���б�ǵĹ�ϵ�Լ�ֱ�ߵ�λ�ù�ϵ�ֱ��ж����ɣ�
��� �⣺��ÿ��ֱ�߶���Ψһһ����б����֮��Ӧ��Ҳ��Ψһһ��б����֮��Ӧ��ֱ��б�ʿ��ܲ����ڣ��ʢٴ���
����б�ǵķ�Χ�ǣ�0��ܦ���180�㣬�ҵ���б������ʱ��б��Ҳ������б�Ǧ���90��ʱ��б���Ǹ�������=90��ʱ�������ڣ��ʢڴ���
�۹�����A��1��2����B��m��-5����ֱ�߿���������ʽ��ʾ�����m=1��б�ʲ����ڣ������������ʾ���ʢ۴���
�ܹ��㣨1��1������б��Ϊ1��ֱ�ߵķ���Ϊ$\frac{y-1}{x-1}=1$��ֱ�߷����ǣ�y-1=x-1����$\frac{y-1}{x-1}=1$��x��1���ʢܴ���
��ֱ��Ax+By+C=0��A��B��ͬʱΪ�㣩����A��B��C����һ��Ϊ��ʱ��������̲��ܻ�Ϊ�ؾ�ʽ���ʢ���ȷ��
������ֱ��ƽ�У������ǵ�б�ʱ���ȣ�б�ʿ��ܲ����ڣ��ʢ���
������ֱ�ߴ�ֱ�������ǵ�б����˱ص���-1��б�ʿ��ܲ����ڣ��ʢߴ���
�ʢ���ȷ��
��ѡ��A��
���� ���⿼����ֱ�ߵ���б�ǡ�ֱ�ߵ�б�����⣬����ֱ�ߵ�λ�ù�ϵ����һ�������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
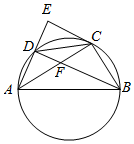 ��ͼ���ı���ABCD�����Բ��AC��Բ�ܽǡ�BAD�Ľ�ƽ���ߣ�����C��������AD�ӳ��߽��ڵ�E��AC��BD�ڵ�F��
��ͼ���ı���ABCD�����Բ��AC��Բ�ܽǡ�BAD�Ľ�ƽ���ߣ�����C��������AD�ӳ��߽��ڵ�E��AC��BD�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -1 | C�� | 0 | D�� | ��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x-2��2+��y+1��2=4 | B�� | ��x+2��2+��y-1��2=4 | C�� | ��x-2��2+��y+1��2=16 | D�� | ��x+2��2+��y-1��2=16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com