
| A. | $\frac{5}{12}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{12}$ | D. | $\frac{3}{4}$ |
分析 根据题意,“事件A,B中至少有一件发生”与“事件A、B一个都不发生”互为对立事件,由古典概型的计算方法,可得P(A)、P(B),进而可得P($\overline{A}$•$\overline{B}$),由对立事件的概率计算,可得答案.
解答 解:根据题意,“事件A,B中至少有一件发生”与“事件A、B一个都不发生”互为对立事件,
由古典概型的计算方法,可得P(A)=$\frac{1}{2}$,P(B)=$\frac{1}{6}$,
则P($\overline{A}$•$\overline{B}$)=(1-$\frac{1}{2}$)(1-$\frac{1}{6}$)=$\frac{5}{12}$,
则“事件A,B中至少有一件发生”的概率为1-$\frac{5}{12}$=$\frac{7}{12}$.
故选C.
点评 本题考查相互独立事件的概率的乘法公式,注意分析题意,首先明确事件之间的相互关系(互斥、对立等).


科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | $\sqrt{29}$ | C. | 5 | D. | $2\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-6-4$\sqrt{2}$,0)∪(0,+∞) | B. | (-6+4$\sqrt{2}$,0)∪(0,+∞) | C. | (-6+4$\sqrt{2}$,0) | D. | (-6-4$\sqrt{2}$,-6+4$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
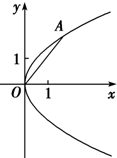 如图,在平面直角坐标系xoy中,抛物线C的顶点在原点,经过点A(2,4),其焦点F在x轴上.
如图,在平面直角坐标系xoy中,抛物线C的顶点在原点,经过点A(2,4),其焦点F在x轴上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
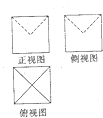 某几何体的三视图如图所示,图中的四边形是边长为2的正方形,其中正视图、侧视图中的两条虚线互相垂直,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形是边长为2的正方形,其中正视图、侧视图中的两条虚线互相垂直,则该几何体的体积是( )| A. | $\frac{20}{3}$ | B. | 6 | C. | $\frac{16}{3}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{1}{2}$个单位长度 | B. | 向右平移$\frac{π}{6}$个单位长度 | ||
| C. | 向左平移$\frac{1}{2}$个单位长度 | D. | 向左平移$\frac{π}{6}$个单位长度 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com