考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)利用三棱锥B1-ABC的体积和三棱柱ABC-A1B1C1的体积公式能直接写出结果.
(Ⅱ)连结C1B,A1B,得到EF∥A1B,由此能证明EF∥平面ABB1A1.
(Ⅲ)取AC中点O,连结B1O,BO,得到OB=OA=OC,B1O⊥AC,从而△B1OA≌△B1OB,由此能证明平面B1AC⊥底面ABC.
解答:
(Ⅰ)解:∵三棱锥B
1-ABC的体积为1,
∴三棱柱ABC-A
1B
1C
1的体积为3.
(Ⅱ)证明:连结C
1B,A
1B,
∵棱柱侧面是平行四边形,
∴线段B
1C的中点E是线段C
1B的中点,
又F是线段A
1C
1的中点,
∴在△C
1A
1B中,EF∥A
1B,又EF?平面ABB
1A
1,
∴EF∥平面ABB
1A
1.
(Ⅲ)证明:取AC中点O,连结B
1O,BO,
∵AB⊥BC,∴OB=OA=OC,
∵AB
1=B
1B
1,∴B
1O⊥AC,
又∵B
1B=AB
1,
∴△B
1OA≌△B
1OB,∴B
1O⊥OB,
∵AC∩OB=O,∴B
1O⊥平面ABC,
∵B
1O?B
1AC,
∴平面B
1AC⊥底面ABC.
点评:本题考查三棱柱的体积的求法,考查线面平行、面面垂直的证明,是中档题,解题时要注意空间中线线、线面、面面间的位置关系和性质的合理运用.

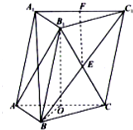
 已知三棱柱ABC-A1B1C1.
已知三棱柱ABC-A1B1C1.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案