Question

8．如图所示，在正方体ABCD-A₁B₁C₁D₁中，E为DD₁上一点，且DE=$\frac{1}{3}$DD₁，F是侧面CDD₁C₁上的动点，且B₁F∥平面A₁BE，则B₁F与平面CDD₁C₁所成角的正切值构成的集合是（　　）

• A． {$\frac{3}{2}$}
• B． {$\frac{2}{5}\sqrt{13}$}
• C． {m|$\frac{3}{2}$≤m≤$\frac{3}{2}$$\sqrt{2}$}
• D． {m|$\frac{2}{5}$$\sqrt{13}$≤m≤$\frac{3}{2}$}

Answer 1

分析 分别在CC₁、C₁D₁上取点N、M，使得CN=$\frac{1}{3}$CC₁，D₁M=$\frac{1}{3}$D₁C₁，连接B₁N、B₁M，可证明平面MNB₁∥平面A₁BE，由B₁F∥平面A₁BE知点F在线段MN上，易证∠B₁FC₁为B₁F与平面CDD₁C₁所成角，tan∠B₁FC₁=$\frac{{B}_{1}{C}_{1}}{{C}_{1}F}$，设出棱长，可求得C₁F的最大值、最小值，从而可得答案．

解答 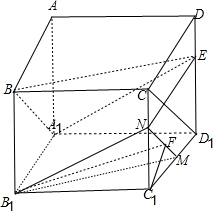解：如图：分别在CC₁、C₁D₁上取点N、M，
使得CN=$\frac{1}{3}$CC₁，D₁M=$\frac{1}{3}$D₁C₁，连接B₁N、B₁M，则MN∥CD₁，
∵BC∥AD，BC=AD，AD∥A₁D₁，AD=A₁D₁，∴BC∥A₁D₁，BC=A₁D₁，
∴四边形BCD₁A₁为平行四边形，则CD₁∥BA₁，
∴MN∥BA₁，
∵CN=$\frac{1}{3}$CC₁，DE=$\frac{1}{3}$DD₁，∴NE∥C₁D₁，NE=C₁D₁，
又C₁D₁∥A₁B₁，C₁D₁=A₁B₁，
∴NE∥A₁B₁，NE=A₁B₁，
∴四边形NEA₁B₁为平行四边形，则B₁N∥A₁E，
且MN∩B₁N=N，
∴平面MNB₁∥平面A₁BE，
∵B₁F∥平面A₁BE，点F必在线段MN上，
连接C₁F，∵B₁C₁⊥平面CDD₁C₁，∴∠B₁FC₁即为B₁F与平面CDD₁C₁所成角，
设正方体棱长为3，则C₁N=C₁M=2，当F为MN中点时，C₁F最短为$\sqrt{2}$，
当F与M或N重合时，C₁F最长为2，
tan∠B₁FC₁=$\frac{{B}_{1}{C}_{1}}{{C}_{1}F}$∈[$\frac{3}{2}$，$\frac{3\sqrt{2}}{2}$]，即所求正切值的取值范围是[$\frac{3}{2}$，$\frac{3\sqrt{2}}{2}$]．
故选：C．

点评 本题考查直线与平面所成的角、面面平行的判定及性质，考查学生分析问题解决问题的能力及空间想象能力．