
| A. | $\frac{\sqrt{5}}{5}$ | B. | -$\frac{1}{2}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | -$\frac{2\sqrt{5}}{5}$ |
分析 利用两角差的正弦函数公式化简可得$\sqrt{5}$sin(x-θ)=$\sqrt{5}$sin(x+φ),(其中,tanθ=2),解得:φ=-θ+2kπ,k∈Z,利用诱导公式可求cosφ的值.
解答 解:∵f(x)=sinx-2cosx=$\sqrt{5}$($\frac{1}{\sqrt{5}}$sinx-$\frac{2}{\sqrt{5}}$cosx)=$\sqrt{5}$sin(x-θ)=$\sqrt{5}$sin(x+φ),(其中,tanθ=2),
∴解得:φ=-θ+2kπ,k∈Z,
∴cosφ=cos(-θ+2kπ)=cosθ=$\frac{\sqrt{5}}{5}$,
故选:A.
点评 本题主要考查了三角函数恒等变换的应用.考查了学生对三角函数基础知识的灵活运用,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b-\frac{2}{3}$$\overrightarrow c$ | B. | -$\frac{2}{3}\overrightarrow a+\frac{1}{2}\overrightarrow b+\frac{1}{2}$$\overrightarrow c$ | C. | $\frac{1}{2}\overrightarrow a-\frac{2}{3}\overrightarrow b+\frac{1}{2}$$\overrightarrow c$ | D. | $\frac{2}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b-\frac{1}{2}$$\overrightarrow c$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | (-∞,-2]∪[2,+∞) | C. | [-2,+∞) | D. | [-2,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ab<b2 | B. | ($\frac{1}{2}$)a>($\frac{1}{2}$)b | ||
| C. | log${\;}_{\frac{1}{2}}$a>log${\;}_{\frac{1}{2}}$b | D. | a2>b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
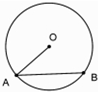
| A. | 18 | B. | -18 | C. | 36 | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5000名学生是总体 | B. | 250名学生是总体的一个样本 | ||
| C. | 样本容量是250 | D. | 每一名学生是个体 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 135° | D. | 45°或135° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com