
设数列{an}的前n项和为Sn.若对任意的正整数n,总存在正整数m,使得Sn=am,则称{an}是“H数列”.
(1)若数列{an}的前n项和Sn=2n(n∈N*),证明:{an}是“H数列”;
(2)设{an}是等差数列,其首项a1=1,公差d<0.若{an}是“H数列”,求d的值;
(3)证明:对任意的等差数列{an},总存在两个“H数列”{bn}和{cn},使得an=bn+cn(n∈N*)成立.
解 (1)首先a1=S1=2,当n≥2时,an=Sn-Sn-1=2n-2n-1=2n-1,∴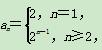
∴对于任意的n∈N*,Sn=2n是数列{an}中的n+1项,因此数列{an}是“H数列”.
(2)由题意an=1+(n-1)d,Sn=n+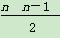 d,数列{an}是“H数列”,则存在k∈N*,使n+
d,数列{an}是“H数列”,则存在k∈N*,使n+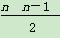 d=1+(k-1)d,k=
d=1+(k-1)d,k=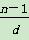 +
+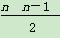 +1,由于
+1,由于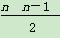 ∈N*,又k∈N*,则
∈N*,又k∈N*,则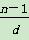 ∈Z对一切正整数n都成立,∴d=-1.
∈Z对一切正整数n都成立,∴d=-1.
(3)若dn=bn(b是常数),则数列{dn}前n项和为Sn=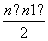 b是数列{dn}中的第
b是数列{dn}中的第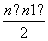 项,因此{dn}是“H数列”,对任意的等差数列{an},an=a1+(n-1)d(d是公差),设bn=na1,cn=(d-a1)(n-1),则an=bn+cn,而数列{bn},{cn}都是“H数列”.
项,因此{dn}是“H数列”,对任意的等差数列{an},an=a1+(n-1)d(d是公差),设bn=na1,cn=(d-a1)(n-1),则an=bn+cn,而数列{bn},{cn}都是“H数列”.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
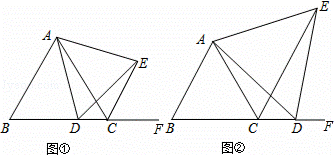
已知等边△ABC,点D是直线BC上一点,以AD为边在AD的右侧作等边△ADE,连结CE.
(1)如图①,若点D在线段BC上,求证:CE+CD=AB;
(2)如图②,若点D在BC延长线上,线段CD,CE和AB有怎样的数量关系?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}的前n项和Sn=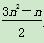 ,n∈N*.
,n∈N*.
(1)求数列{an}的通项公式;
(2)证明:对任意的n>1,都存在m∈N*,使得a1,an,am成等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
观察下列算式:
13=1,
23=3+5,
33=7+9+11,
43=13+15+17+19,
……
若某数m3按上述规律展开后,发现等式右边含有“2 013”这个数,则m=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com