
分析 (1)根据抛物线的定义得出轨迹方程;
(2)设出P点坐标(x,y),将$\overrightarrow{PD}$•$\overrightarrow{PF}$表示为x(或y)的函数,根据函数性质求出最小值;
(3)设A坐标(0,b)和直线l的斜率k,根据相切得出k,b的关系,求出M,N坐标得出圆C的圆心和半径,利用切线的性质得出AB的长.
解答 解:(I)由题意可知曲线E为以F为焦点,以直线x=-1为准线的抛物线,
∴曲线E的方程为y2=4x.
(II)设P($\frac{{y}^{2}}{4}$,y),则$\overrightarrow{PD}=(2-\frac{{y}^{2}}{4},-y)$,$\overrightarrow{PF}=(1-\frac{{y}^{2}}{4},-y)$,
∴$\overrightarrow{PD}•\overrightarrow{PF}$=(2-$\frac{{y}^{2}}{4}$)(1-$\frac{{y}^{2}}{4}$)+y2=$\frac{1}{16}$(y2+2)2+$\frac{7}{4}$.
∵y2≥0,
∴当y2=0时,$\overrightarrow{PD}•\overrightarrow{PF}$取得最小值2.
(III)设A(0,b),
显然x=0为抛物线E的一条切线,此时,x=0与x=3无交点,
故点M不存在,不符合题意,
设抛物线E的另一条切线l的方程为y=kx+b,
联立方程组$\left\{\begin{array}{l}{y=kx+b}\\{{y}^{2}=4x}\end{array}\right.$,消元得k2x2+(2kb-4)x+b2=0,
∵直线l与曲线C相切,
∴△=(2kb-4)2-4k2b2=0,即kb=1.∴k=$\frac{1}{b}$.
∴直线l的方程为y=$\frac{1}{b}x+b$,
令x=3得y=b+$\frac{3}{b}$.
∴M(3,b+$\frac{3}{b}$),N(3,0).
∴以MN为直径的圆C的圆心为C(3,$\frac{b}{2}$+$\frac{3}{2b}$),半径r=|$\frac{b}{2}+\frac{3}{2b}$|,
∴AC2=9+($\frac{3}{2b}$-$\frac{b}{2}$)2.
∵AB是圆C的切线,∴AB2=AC2-BC2=AC2-r2=6.
∴AB=$\sqrt{6}$.
即点A在y轴上运动(点A与原点不重合)时,线段AB的长度不发生变化.
点评 本题考查了抛物线的定义,向量的数量积运算,直线与圆锥曲线的关系,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 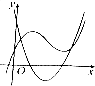 | B. | 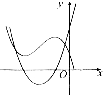 | C. | 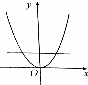 | D. | 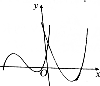 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向左平移$\frac{π}{3}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 产假安排(单位:周) | 14 | 15 | 16 | 17 | 18 |
| 有生育意愿家庭数 | 4 | 8 | 16 | 20 | 26 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com