
【题目】在△ABC中,a,b,c分别为角A,B,C的对边.若acosB=3,bcosA=l,且A﹣B= ![]()
(1)求边c的长;
(2)求角B的大小.
【答案】
(1)解:∵acosB=3,bcosA=l,∴a× ![]() =3,b×
=3,b× ![]() =1,
=1,
化为:a2+c2﹣b2=6c,b2+c2﹣a2=2c.
相加可得:2c2=8c,解得c=4
(2)解:由(1)可得:a2﹣b2=8.
由正弦定理可得: ![]() =
= ![]() =
= ![]() ,
,
又A﹣B= ![]() ,∴A=B+
,∴A=B+ ![]() ,C=π﹣(A+B)=
,C=π﹣(A+B)= ![]() ,可得sinC=sin
,可得sinC=sin ![]() .
.
∴a= 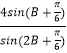 ,b=
,b= ![]() .
.
∴ ![]() ﹣16sin2B=
﹣16sin2B= ![]() ,
,
∴1﹣ ![]() ﹣(1﹣cos2B)=
﹣(1﹣cos2B)= ![]() ,即cos2B﹣
,即cos2B﹣ ![]() =
= ![]() ,
,
∴﹣2 ![]() ═
═ ![]() ,
,
∴ ![]() =0或
=0或 ![]() =1,B∈
=1,B∈ ![]() .
.
解得:B= ![]()
【解析】(1)由acosB=3,bcosA=l,利用余弦定理化为:a2+c2﹣b2=6c,b2+c2﹣a2=2c.相加即可得出c.(2)由(1)可得:a2﹣b2=8.由正弦定理可得: ![]() =
= ![]() =
= ![]() ,又A﹣B=
,又A﹣B= ![]() ,可得A=B+
,可得A=B+ ![]() ,C=
,C= ![]() ,可得sinC=sin
,可得sinC=sin ![]() .代入可得
.代入可得 ![]() ﹣16sin2B=
﹣16sin2B= ![]() ,化简即可得出.
,化简即可得出.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 其中实数
其中实数![]() 为常数且
为常数且![]() .
.
(I)求函数![]() 的单调区间;
的单调区间;
(II)若函数![]() 既有极大值,又有极小值,求实数
既有极大值,又有极小值,求实数![]() 的取值范围及所有极值之和;
的取值范围及所有极值之和;
(III)在(II)的条件下,记![]() 分别为函数
分别为函数![]() 的极大值点和极小值点,
的极大值点和极小值点,
求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为 . 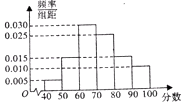
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某环保节能设备生产企业的产品供不应求,已知某种设备的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=150﹣ ![]() x,每套的售价不低于90万元;月产量x(套)与生产总成本y2(万元)之间满足关系式y2=600+72x,则月生产多少套时,每套设备的平均利润最大?最大平均利润是多少?
x,每套的售价不低于90万元;月产量x(套)与生产总成本y2(万元)之间满足关系式y2=600+72x,则月生产多少套时,每套设备的平均利润最大?最大平均利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
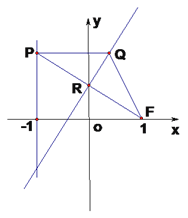
【题目】在平面直角坐标系![]() 中,设点
中,设点![]() (1,0),直线
(1,0),直线![]() :
: ![]() ,点
,点![]() 在直线
在直线![]() 上移动,
上移动, ![]() 是线段
是线段![]() 与
与![]() 轴的交点, 异于点R的点Q满足:
轴的交点, 异于点R的点Q满足: ![]() ,
, ![]() .
.
(1)求动点![]() 的轨迹的方程;
的轨迹的方程;
(2) 记![]() 的轨迹的方程为
的轨迹的方程为![]() ,过点
,过点![]() 作两条互相垂直的曲线
作两条互相垂直的曲线![]()
的弦![]() .
. ![]() ,设
,设![]() .
. ![]() 的中点分别为
的中点分别为![]() .
.
问直线![]() 是否经过某个定点?如果是,求出该定点,
是否经过某个定点?如果是,求出该定点,
如果不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是正四面体的平面展开图,G、H、M、N分别为DE、BE、EF、EC的中点,在这个正四面体中,
①GH与EF平行;②BD与MN为异面直线;③GH与MN成60°角;④DE与MN垂直.以上四个命题中,正确命题的序号是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:2ax+y﹣1=0,l2:ax+(a﹣1)y+1=0,
(1)若l1⊥l2 , 求实数a的值;
(2)若l1∥l2时,求直线l1与l2之间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com