练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．设x＞0，y＞0，向量$\overrightarrow a$=（1-x，4），$\overrightarrow b$=（x，-y），若$\overrightarrow a$∥$\overrightarrow b$，则x+y的最小值为9．

    分析 先根据向量平行得到$\frac{1}{x}$+$\frac{4}{y}$=1，再利用基本不等式即可求出最值．

    解答 解：因为$\overrightarrow a$∥$\overrightarrow b$，
    所以4x+（1-x）y=0，
    又x＞0，y＞0，
    所以$\frac{1}{x}$+$\frac{4}{y}$=1，
    故x+y=（$\frac{1}{x}$+$\frac{4}{y}$）（x+y）=5+$\frac{y}{x}$+$\frac{4x}{y}$≥9．
    当$\frac{y}{x}$=$\frac{4x}{y}$，$\frac{1}{x}$+$\frac{4}{y}$=1同时成立，即x=3，y=6时，等号成立．
    （x+y）min=9．
    故答案为：9．

    点评 本题考查了向量平行的条件和基本不等式的应用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    5．如图，在△ABC中，BC边上的中线为AD．
    （1）若AD=BD=2，AB=3，求ABC的面积；
    （2）若∠ABC=30°，∠ACB=45°，求tan∠BAD的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知等差数列{an）的前n项和为Sn=-n2+（10+k）n+（k-1），则实数k=1，an=-2n+12．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．如图所示的流程图，现输入以下函数，则可以输出的函数是（　　）
    A．f（x）=sinxB．f（x）=|x|C．f（x）=$\frac{1}{2}$（2x+2-x）D．f（x）=ln$\frac{2-x}{2+x}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．对一批产品的长度（单位：毫米）进行抽样检测，样本容量为400，右图为检测结果的频率分布直方图，根据产品标准，单件产品长度在区间[25，30）的为一等品，在区间[20，25）和[30，35）的为二等品，其余均为三等品，则样本中三等品的件数为100．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．△ABC中，a，b，c分别为角A，B，C的所对边的长，若acosB=1，bsinA=$\sqrt{2}$，且A-B=$\frac{π}{4}$．
    （1）求a的值；
    （2）求tanA的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．若双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}$=1的离心率为$\sqrt{3}$，则其渐近线方程为y=±$\frac{\sqrt{2}}{2}$x．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．若某几何体的三视图如图所示，则此几何体的体积是（　　）
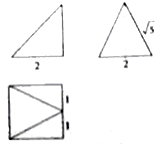
    A．4$\sqrt{5}$B．$\frac{4\sqrt{5}}{3}$C．$\frac{8}{3}$D．$\frac{4}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知集合A={0，1，2，3，4}，集合B={y|y=$\sqrt{x}$，x∈A}．则集合A∩B=（　　）
    A．{0}B．{0，1}C．{0，1，2}D．{0，1，2，4}

    查看答案和解析>>

    同步练习册答案