
分析 先求出函数的导数,根据函数的单调性结合二次函数的性质求出a的范围即可.
解答 解:f′(x)=$\frac{-{ax}^{2}+4x-a}{{(1{-x}^{2})}^{2}}$,
若f(x)在区间[$\frac{1}{3}$,$\frac{1}{2}$]上是单调函数,
只需f′(x)>0或f′(x)<0[$\frac{1}{3}$,$\frac{1}{2}$]在区间[$\frac{1}{3}$,$\frac{1}{2}$]上恒成立即可,
a=0时,f′(x)>0在区间[$\frac{1}{3}$,$\frac{1}{2}$]上恒成立,
a≠0时,$\left\{\begin{array}{l}{-a>0}\\{\frac{2}{a}<0}\\{f′(\frac{1}{3})=-\frac{10}{9}a+\frac{4}{3}≥0}\end{array}\right.$或$\left\{\begin{array}{l}{-a<0}\\{△=\frac{2}{a}>0}\\{f′(\frac{1}{3})f′(\frac{1}{2})=(-\frac{10}{9}a+\frac{4}{3})(-\frac{5}{4}a+2)>0}\end{array}\right.$,
解得:a>$\frac{12}{5}$或a<$\frac{4}{5}$,
综上,a∈(-∞,$\frac{4}{5}$)∪($\frac{12}{5}$,+∞).
点评 本题考查了函数的单调性问题,考查导数的应用,考查二次函数的性质,是一道中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
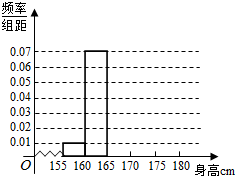 某校为了调查学生身体生长发育情况,随机抽取200名学生测得它们的身高(单位:cm),并按照区间[155,160),[160,165),[165,170),[170,175),[175,180)分组,得到样本的频率分布直方图.由于操作不慎,区间[165,170),[170,175),[175,180)的频率分布直方图被破坏了,如图所示.已知频率分布直方图中[165,170),[170,175),[175,180)间的矩形的高依次成等差数列,并且身高在[170,175)内的人数是身高在[175,180)的人数的2倍.
某校为了调查学生身体生长发育情况,随机抽取200名学生测得它们的身高(单位:cm),并按照区间[155,160),[160,165),[165,170),[170,175),[175,180)分组,得到样本的频率分布直方图.由于操作不慎,区间[165,170),[170,175),[175,180)的频率分布直方图被破坏了,如图所示.已知频率分布直方图中[165,170),[170,175),[175,180)间的矩形的高依次成等差数列,并且身高在[170,175)内的人数是身高在[175,180)的人数的2倍.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{9}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com