
分析 先分离参数得到$a=\frac{x}{x-lnx}-\frac{lnx}{x}$,令h(x)=$\frac{x}{x-lnx}-\frac{lnx}{x}$.求导后得其极值点,求得函数极值,则使h(x)恰有三个零点的实数a的取值范围由a=$\frac{x}{x-lnx}-\frac{lnx}{x}$=$\frac{1}{1-\frac{lnx}{x}}-\frac{lnx}{x}$,再令$μ=\frac{lnx}{x}$,转化为关于μ的方程后由根与系数关系得到μ1+μ2=1-a<0,μ1μ2=1-a<0,再结合着$μ=\frac{lnx}{x}$的图象可得到$(1-\frac{ln{x}_{1}}{{x}_{1}})^{2}(1-\frac{ln{x}_{2}}{{x}_{2}})(1-\frac{ln{x}_{3}}{{x}_{3}})$=1.
解答  解:由f(x)=ax+lnx-$\frac{{x}^{2}}{x-lnx}$=0分离参数得$a=\frac{x}{x-lnx}-\frac{lnx}{x}$,
解:由f(x)=ax+lnx-$\frac{{x}^{2}}{x-lnx}$=0分离参数得$a=\frac{x}{x-lnx}-\frac{lnx}{x}$,
令h(x)=$\frac{x}{x-lnx}-\frac{lnx}{x}$,
由h′(x)=$\frac{1-lnx}{(x-lnx)^{2}}-\frac{1-lnx}{{x}^{2}}$=$\frac{lnx(1-lnx)(2x-lnx)}{{x}^{2}(x-lnx)^{2}}$=0,得x=1或x=e.
当x∈(0,1)时,h′(x)<0;
当x∈(1,e)时,h′(x)>0;
当x∈(e,+∞)时,h′(x)<0.
即h(x)在(0,1),(e,+∞)上为减函数,在(1,e)上为增函数.
而当x→0,h(x)→+∞,当x→+∞,h(x)→1,
又h(1)=1,h(e)=$1+\frac{1}{e(e-1)}$;
结合函数的单调性可得,实数a的取值范围为(1,$1+\frac{1}{e(e-1)}$).
则0<x1<1<x2<e<x3,
a=$\frac{x}{x-lnx}-\frac{lnx}{x}$=$\frac{1}{1-\frac{lnx}{x}}-\frac{lnx}{x}$,令$μ=\frac{lnx}{x}$,
则a=$\frac{1}{1-μ}-μ$,即μ2+(a-1)μ+1-a=0,
μ1+μ2=1-a<0,μ1μ2=1-a<0,
对于$μ=\frac{lnx}{x}$,$μ′=\frac{1-lnx}{{x}^{2}}$
则当0<x<e时,μ′>0;当x>e时,μ′<0.而当x>e时,μ恒大于0.
画其简图,
不妨设μ1<μ2,则${μ}_{1}=\frac{ln{x}_{1}}{{x}_{1}},{μ}_{2}=\frac{ln{x}_{2}}{{x}_{2}}=\frac{ln{x}_{3}}{{x}_{3}}$,
∴$(1-\frac{ln{x}_{1}}{{x}_{1}})^{2}(1-\frac{ln{x}_{2}}{{x}_{2}})(1-\frac{ln{x}_{3}}{{x}_{3}})$=$(1-{μ}_{1})^{2}(1-{μ}_{2})(1-{μ}_{2})$=$[(1-{μ}_{1})(1-{μ}_{2})]^{2}$
=$[1-({μ}_{1}+{μ}_{2})+{μ}_{1}{μ}_{2}]^{2}$=[1-(1-a)+(1-a)]2=1
故答案为:1
点评 本题考查了利用函数研究函数单调性,极值等性质,训练了函数零点的判断方法,运用了分离变量法,换元法,函数构造法等数学转化思想方法,综合性强难度较大.


科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 1 | C. | -1 | D. | 1或-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
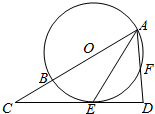 如图所示,⊙O的圆心O在Rt△ACD的斜边AC上,且⊙O过顶点A,与边CD相切于点E,与边AD、AC分别相交于点F,B.
如图所示,⊙O的圆心O在Rt△ACD的斜边AC上,且⊙O过顶点A,与边CD相切于点E,与边AD、AC分别相交于点F,B.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
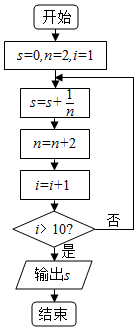
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x2 | B. | f(x)=x | C. | f(x)=$\sqrt{x}$ | D. | f(x)=$\frac{1}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=2sin(ωx+$\frac{π}{4}$)在一个周期内的图象如图所示.
已知函数f(x)=2sin(ωx+$\frac{π}{4}$)在一个周期内的图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com