
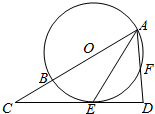
 如图所示,⊙O的圆心O在Rt△ACD的斜边AC上,且⊙O过顶点A,与边CD相切于点E,与边AD、AC分别相交于点F,B.
如图所示,⊙O的圆心O在Rt△ACD的斜边AC上,且⊙O过顶点A,与边CD相切于点E,与边AD、AC分别相交于点F,B.分析 (1)连接OE,则OE⊥CD,证明∠DAE=∠OAE,即可证明AE是∠CAD的平分线;
(2)若CE=10,CB=5,由切割线定理求出CA,利用余弦定理求AE的长.
解答 (1)证明:连接OE,则OE⊥CD,
∵AD⊥CD,
∴OE∥AD,
∴∠OEA=∠DAE,
∵OA=OE,
∴∠OEA=∠OAE,
∴∠DAE=∠OAE,
∴AE是∠CAD的平分线;
(2)解:若CE=10,CB=5,由切割线定理,可得102=5•CA,
∴CA=20,
∴OA=OB=7.5,
∴cos∠COE=$\frac{7.5}{12.5}$=$\frac{4}{5}$
△OAE中,AE=$\sqrt{7.{5}^{2}+7.{5}^{2}-2×7.5×7.5×(-\frac{4}{5})}$=$\frac{9}{2}\sqrt{10}$.
点评 本题考查圆的切线的性质,考查切割线定理、余弦定理,考查学生分析解决问题的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
| x | $\frac{2π}{3}$ | $\frac{5π}{6}$ | |||
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| Asin(ωx+φ) | 0 | 2 | 0 | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
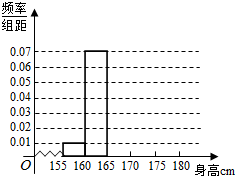 某校为了调查学生身体生长发育情况,随机抽取200名学生测得它们的身高(单位:cm),并按照区间[155,160),[160,165),[165,170),[170,175),[175,180)分组,得到样本的频率分布直方图.由于操作不慎,区间[165,170),[170,175),[175,180)的频率分布直方图被破坏了,如图所示.已知频率分布直方图中[165,170),[170,175),[175,180)间的矩形的高依次成等差数列,并且身高在[170,175)内的人数是身高在[175,180)的人数的2倍.
某校为了调查学生身体生长发育情况,随机抽取200名学生测得它们的身高(单位:cm),并按照区间[155,160),[160,165),[165,170),[170,175),[175,180)分组,得到样本的频率分布直方图.由于操作不慎,区间[165,170),[170,175),[175,180)的频率分布直方图被破坏了,如图所示.已知频率分布直方图中[165,170),[170,175),[175,180)间的矩形的高依次成等差数列,并且身高在[170,175)内的人数是身高在[175,180)的人数的2倍.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{9}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com