
分析 将2|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|2$\overrightarrow{a}-\overrightarrow{b}$|两边平方,得出$\overrightarrow{a}•\overrightarrow{b}$与|$\overrightarrow{a}$|的关系,计算|$\overrightarrow{a}+\overrightarrow{b}$|和$\overrightarrow{a}•(\overrightarrow{a}+\overrightarrow{b})$,代入夹角公式计算.
解答 解:∵2|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|2$\overrightarrow{a}-\overrightarrow{b}$|,∴4${\overrightarrow{a}}^{2}$=${\overrightarrow{b}}^{2}$=4${\overrightarrow{a}}^{2}$-4$\overrightarrow{a}•\overrightarrow{b}$+${\overrightarrow{b}}^{2}$,∴$\overrightarrow{a}•\overrightarrow{b}$=$\frac{{\overrightarrow{b}}^{2}}{4}$=${\overrightarrow{a}}^{2}$.
∴|$\overrightarrow{a}+\overrightarrow{b}$|2=${\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}$=7${\overrightarrow{a}}^{2}$.∴|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{7}$|$\overrightarrow{a}$|.
$\overrightarrow{a}•(\overrightarrow{a}+\overrightarrow{b})$=${\overrightarrow{a}}^{2}+\overrightarrow{a}•\overrightarrow{b}$=2${\overrightarrow{a}}^{2}$.
∴cos<$\overrightarrow{a}$,$\overrightarrow{a}+\overrightarrow{b}$>=$\frac{\overrightarrow{a}•(\overrightarrow{a}+\overrightarrow{b})}{|\overrightarrow{a}||\overrightarrow{a}+\overrightarrow{b}|}$=$\frac{2{\overrightarrow{a}}^{2}}{\sqrt{7}|\overrightarrow{a}{|}^{2}}$=$\frac{2\sqrt{7}}{7}$.
故答案为:$\frac{2\sqrt{7}}{7}$.
点评 本题考查了平面向量的数量积运算,模长计算,属于基础题.


科目:高中数学 来源: 题型:解答题
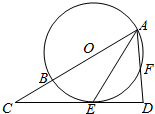 如图所示,⊙O的圆心O在Rt△ACD的斜边AC上,且⊙O过顶点A,与边CD相切于点E,与边AD、AC分别相交于点F,B.
如图所示,⊙O的圆心O在Rt△ACD的斜边AC上,且⊙O过顶点A,与边CD相切于点E,与边AD、AC分别相交于点F,B.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=2sin(ωx+$\frac{π}{4}$)在一个周期内的图象如图所示.
已知函数f(x)=2sin(ωx+$\frac{π}{4}$)在一个周期内的图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6$\sqrt{5}$ | B. | 12 | C. | 6$\sqrt{3}$ | D. | 6$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{△-4}{△+4}$ | B. | $\frac{\sqrt{△}-2}{\sqrt{△}+2}$ | C. | $\frac{△+4}{△-4}$ | D. | $\frac{\sqrt{△}+2}{\sqrt{△}-2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com