Question

5．过圆锥顶点的截面均为等腰三角形，两腰都是母线，这些截面以轴截面的面积为最大，对吗？

Answer 1

分析 设圆锥底面半径为r，高为h，截面与底面的交线为AB，设AB=x，用x表示出截面的面积S_△SAB，利用不等式得出截面面积的最大值及等号成立的条件．

解答 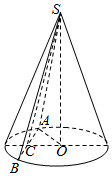解：设圆锥截面SAB与底面交于A，B两点，
∵SA=SB，∴△SAB是等腰三角形．
设圆锥的底面半径为OA=r，高SO=h，
过O作OC⊥AB于C，则C为AB的中点．
∴SC⊥AB．
设AB=x，则AC=$\frac{1}{2}AB=\frac{x}{2}$．
由垂径定理得OC=$\sqrt{O{A}^{2}-A{C}^{2}}$=$\sqrt{{r}^{2}-\frac{{x}^{2}}{4}}$．
∴SC=$\sqrt{S{O}^{2}+O{C}^{2}}$=$\sqrt{{h}^{2}+{r}^{2}-\frac{{x}^{2}}{4}}$．
∴S_△SAB=$\frac{1}{2}AB•SC$=$\frac{1}{2}$x$\sqrt{{h}^{2}+{r}^{2}-\frac{{x}^{2}}{4}}$=$\sqrt{\frac{{x}^{2}}{4}（{h}^{2}+{r}^{2}-\frac{{x}^{2}}{4}）}$≤$\sqrt{（\frac{\frac{{x}^{2}}{4}+{h}^{2}+{r}^{2}-\frac{{x}^{2}}{4}}{2}）^{2}}$=$\frac{{h}^{2}+{r}^{2}}{2}$．
当且仅当$\frac{{x}^{2}}{4}={h}^{2}+{r}^{2}-\frac{{x}^{2}}{4}$，即x=$\sqrt{2{h}^{2}+2{r}^{2}}$时取等号．
所以上述命题中，前两个命题正确，第三个命题错误．

点评 本题考查了圆锥的结构特征，基本不等式的应用，属于中档题．