
| A. | (-∞,$\frac{1}{2}$] | B. | (-∞,$\frac{1}{2}$) | C. | (-∞,1] | D. | (-∞,1) |
分析 把已知的数列递推式变形,得到$\frac{{a}_{n+1}}{{a}_{n}}=\frac{n}{n+1}$,然后利用累积法求得数列{an}的通项公式,再由错位相减法求得数列{anan+1}的前n项和,最后由数列的函数特性得答案.
解答 解:由(n+1)an+12-nan2+an+1an=0,得:
(an+1+an)[(n+1)an+1-nan]=0,
∵an>0,∴(n+1)an+1-nan=0,则$\frac{{a}_{n+1}}{{a}_{n}}=\frac{n}{n+1}$.
∴${a}_{n}=\frac{n-1}{n}•\frac{n-2}{n-1}…\frac{1}{2}•1=\frac{1}{n}$.
则a1•a2+a2•a3+…+an•an+1=$\frac{1}{1}•\frac{1}{2}+\frac{1}{2}•\frac{1}{3}+$…+$\frac{1}{n}•\frac{1}{n+1}$
=1$-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+$…+$\frac{1}{n}-\frac{1}{n+1}$=$1-\frac{1}{n+1}$.
∵a1•a2+a2•a3+…+an•an+1≥m对任意n∈N*恒成立,
∴m$≤1-\frac{1}{2}=\frac{1}{2}$.
则实数m的取值范围是:(-∞,$\frac{1}{2}$].
故选:A.
点评 本题考查了数列递推式,训练了累积法求数列的通项公式,考查了错位相减法求数列的和,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4π | B. | 2π | C. | π | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
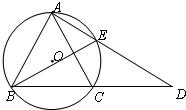 如图,⊙O是△ABC的外接圆,AB=AC,延长BC到点D,使得CD=AC,连结AD交⊙O于点E,连结BE,若∠D=35°,则∠ABE的大小为35°.
如图,⊙O是△ABC的外接圆,AB=AC,延长BC到点D,使得CD=AC,连结AD交⊙O于点E,连结BE,若∠D=35°,则∠ABE的大小为35°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com