
分析 (1)不等式x2+px>4x+p-4化为x2+(p-4)x+4-p>0①,设f(x)=x2+(p-4)x+4-p,不等式①在2≤x≤4时有解时,f(2)>0,或f(4)>0,由此求出p的取值范围;
(2)不等式x2+px>(4x+p-4)化为p(x-1)+(x2-4x+4)>0②,设g(p)=p(x-1)+(x2-4x+4),0≤p≤6时不等式②恒成立,得$\left\{\begin{array}{l}{g(0)>0}\\{g(6)>0}\end{array}\right.$,求出x的取值范围即可.
解答 解:(1)不等式x2+px>4x+p-4可化为x2+(p-4)x+4-p>0①,
设f(x)=x2+(p-4)x+4-p,
当不等式①在2≤x≤4时有解时,
即存在x∈[2,4],使f(x)>0,
所以f(2)>0,或f(4)>0成立,
即4+2(p-4)+4-p>0,或16+4(p-4)+4-p>0,
解得p>-$\frac{3}{4}$;
(2)不等式x2+px>(4x+p-4)化为p(x-1)+(x2-4x+4)>0②,
设g(p)=p(x-1)+(x2-4x+4),
因为0≤p≤6时不等式②恒成立,
即$\left\{\begin{array}{l}{g(0)>0}\\{g(6)>0}\end{array}\right.$,
所以$\left\{\begin{array}{l}{{x}^{2}-4x+4>0}\\{6(x-1){+(x}^{2}-4x+4)>0}\end{array}\right.$,
解得x<-1-$\sqrt{3}$,或x>-1+$\sqrt{3}$,且x≠-2.
点评 本题考查了不等式的恒成立问题,也考查了不等式在某一闭区间上有解的问题,是综合性题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4\sqrt{2}}{9}$ | B. | $\frac{4\sqrt{2}}{9}$ | C. | -$\frac{4\sqrt{2}}{7}$ | D. | $\frac{4\sqrt{2}}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{56}$ | B. | $\frac{9}{28}$ | C. | $\frac{9}{14}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
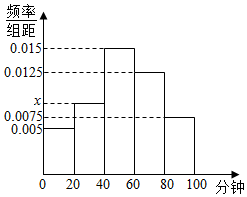 某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图,其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图,其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com