
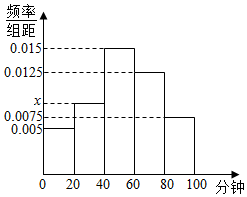
 某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图,其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图,其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].分析 (I)由题意,可由直方图中各个小矩形的面积和为1求出x值.
(II)再求出小矩形的面积即上学所需时间不少于1小时组人数在样本中的频率,再乘以样本容量即可得到此组的人数即可.
解答 解:(Ⅰ)由直方图可得
(x+0.005+0.0075+0.0125+0.015)×20=1.
所以x=0.01.
(Ⅱ)由直方图可知,新生上学所需时间不少于1小时的频率为:(0.0125+0.0075)×20=0.4.
因为 600×0.4=240.
所以 600名新生中有240名学生可以申请住宿.
点评 本题考查频率分布直方图,解题的关键是理解直方图中各个小矩形的面积的意义及各个小矩形的面积和为1,本题考查了识图的能力.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c>a>b | B. | b>a>c | C. | a>b>c | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com